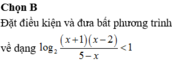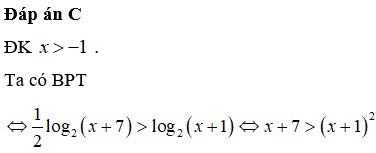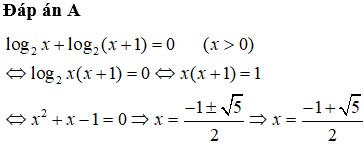giải phương trình log2(5^x+1 - 25^x) = 2
CN
Những câu hỏi liên quan
Giải phương trình log 2 ( x + 1 ) = l o g 2 ( x 2 + 2 ) - 1
A. x = 1
B. x = 0
C. x = 0, x = -4
D. x = 0, x = 1
Tập nghiệm của bất phương trình
log
2
(
x
+
1
)
-
2
log
4
(
5
-
x
)
1
-
log
2
(
x
-
2
)
là A. (3;5) B. (2;3) C. (2;5) D. (-4;3)
Đọc tiếp
Tập nghiệm của bất phương trình log 2 ( x + 1 ) - 2 log 4 ( 5 - x ) < 1 - log 2 ( x - 2 ) là
A. (3;5)
B. (2;3)
C. (2;5)
D. (-4;3)
Giải phương trình log 2 ( 2 + x ) = 2
A. x = 6
B. x = -2
C. x = 4
D. x = 2
Giải bất phương trình log 4 ( x + 7 ) > log 2 ( x + 1 )
A. x> -1
B. x> 5
C. -1< x <2
D. x< 1
Giải phương trình
log
2
x
+
log
2
(
x
+
1
)
0
A.
x
-
1
+
5
2
B.
x
-
1
+
3...
Đọc tiếp
Giải phương trình log 2 x + log 2 ( x + 1 ) = 0
A. x = - 1 + 5 2
B. x = - 1 + 3 2
C. x = 1 + 5 2
D. x = 1 + 3 2
Tìm tập nghiệm của phương trình log2(x - 2) + log2(x+1) = 2
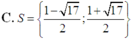
Gọi S1 là tập nghiệm của bất phương trình
log
2
(
x
+
5
)
+
log
1
2
(
3
-
x
)
≥
0
và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ? A.
S
1
∩
S
2
[...
Đọc tiếp
Gọi S1 là tập nghiệm của bất phương trình log 2 ( x + 5 ) + log 1 2 ( 3 - x ) ≥ 0 và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ?
A. S 1 ∩ S 2 = [ 1 ; 3 )
B. S 1 ∩ S 2 = [ - 1 ; 3 )
C. S 1 ∩ S 2 = - 1 ; 1
D. S 1 ∩ S 2 = 1 ; 3
Tìm số nghiệm của phương trình log2 x + log2 (x -1) = 2
A. 0
B. 1
C. 3
D. 2
MN
4 tháng 10 2021 lúc 22:33
Tính tổng tất cả các nghiệm của phương trình: \(\dfrac{1}{2}\).log2(x+3) = log2(x+1) + x2 - x - 4 + 2\(\sqrt{x+3}\)
ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)
Đúng 1
Bình luận (0)