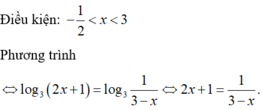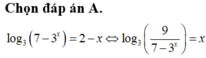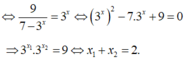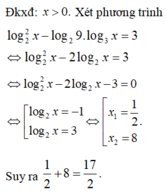Tìm các nghiêm của các phương trình log3(10-x)+1/2logcăn3(x+2)=2 là.
RN
Những câu hỏi liên quan
Tìm số nghiệm của phương trình l o g 3 ( x - 1 ) 2 + l o g 3 ( 2 x - 1 ) = 2
A. 0
B. 3
C. 1
D. 2
Biết x = - 2 là một trong các nghiệm của phương trình: x 3 + a x 2 - 4 x - 4 = 0 . Với a tìm được ở câu a, tìm các nghiêm còn lại của phương trình bằng cách đưa phương trình đã cho về dạng phương trình tích.
Với a = 1, ta có phương trình: x 3 + a x 2 - 4 x - 4 = 0
⇒ x 2 (x + 1) – 4(x + 1) = 0 ⇒ ( x 2 – 4)(x + 1) = 0
⇒ (x + 2)(x – 2)(x + 1) = 0
⇒ x + 2 = 0 hoặc x – 2 = 0 hoặc x + 1 = 0
x + 2 = 0 ⇒ x = -2
x – 2 = 0 ⇒ x = 2
x + 1 = 0 ⇒ x = -1
Vậy phương trình có nghiệm: x = -2 hoặc x = 2 hoặc x = -1.
Đúng 0
Bình luận (0)
Tổng các nghiệm của phương trình l o g 3 ( 7 - 3 x ) = 2 - x bằng
A. 7
B. 2
C. 3
D. 1
Tổng các nghiệm của phương trình
log
3
(
2
x
+
1
)
-
log
1
3
(
3
-
x
)
0
là:
Đọc tiếp
Tổng các nghiệm của phương trình log 3 ( 2 x + 1 ) - log 1 3 ( 3 - x ) = 0 là:
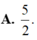

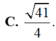
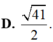
Tổng tất cả các nghiệm của phương trình
log
3
(
7
-
3
x
)
2
-
x
bằng A. 2 B. 1 C. 7 D. 3
Đọc tiếp
Tổng tất cả các nghiệm của phương trình log 3 ( 7 - 3 x ) = 2 - x bằng
A. 2
B. 1
C. 7
D. 3
Tổng tất cả các nghiệm của phương trình l o g 3 ( 7 - 3 x ) = 2 - x bằng
A.1
B.7
C. 2
D. 3
Tổng các nghiệm của phương trình
log
2
2
x
-
log
2
9
.
log
3
x
3
là: A. –2. B. 2. C. 8. D.
17
2
Đọc tiếp
Tổng các nghiệm của phương trình log 2 2 x - log 2 9 . log 3 x = 3 là:
A. –2.
B. 2.
C. 8.
D. 17 2
Biết phương trình log5\(\dfrac{2\sqrt{x}+1}{x}\) = 2.log3\(\left(\dfrac{\sqrt{x}}{2}-\dfrac{1}{2\sqrt{x}}\right)\) có một nghiệm dạng x= a + b\(\sqrt{2}\) trong đó a,b là các số nguyên. Tính 2a+b
Bài này e rằng quá khó để tự luận do vấn đề cơ số
Nhưng tinh ý 1 chút thì giải trắc nghiệm đơn giản:
\(\dfrac{\sqrt{x}}{2}-\dfrac{1}{2\sqrt{x}}=\dfrac{x-1}{2\sqrt{x}}\)
Để ý rằng \(x-1-2\sqrt{x}=x-\left(2\sqrt{x}+1\right)\)
Do đó pt luôn có nghiệm thỏa mãn: \(x-2\sqrt{x}-1=0\Rightarrow x=3+2\sqrt{2}\)
Đúng 0
Bình luận (0)
Tìm tập nghiệm S của phương trình log 3 ( 2 x + 1 ) - log 3 ( x - 1 ) = 1
A. S = {4}
B. S = {3}
C. S = {-2}
D. S = {1}
Tìm tập nghiệm S của phương trình log3( 2x+1) – log3(x-1) = 1
A.S= {4}
B. S= {3}
C. S= {-2}
D. S = {3}