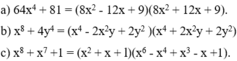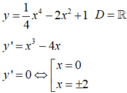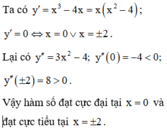phân tich :x8+14x4+1
KH
Những câu hỏi liên quan
Tìm cực đại của hàm số y = − 1 4 x 4 + 2 x 2 − 1.
A.3
B.0
C.-1
D. ± 2
Đáp án A
Ta có y ' = − x 3 + 4 x ⇒ y ' = 0 ⇔ x = 0 x = ± 2 . (Chú ý cực đại là giá trị cực đại ).
Mặt khác y 0 = − 1 y ± 2 = 3 ⇒ y C D = 3.
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:a) x4+4 b) x8+x7+1c) x8+x4+1 d) x5+x+1e) x2+2x2-24 f) a4+4b4
Đọc tiếp
Phân tích đa thức thành nhân tử:
a) x4+4 b) x8+x7+1
c) x8+x4+1 d) x5+x+1
e) x2+2x2-24 f) a4+4b4
a: \(x^4+4=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
b: \(x^8+x^7+1\)
\(=x^8+x^7+x^6-x^6-x^5-x^4+x^5+x^4+x^3-x^3-x^2-x+x^2+x+1\)
\(=\left(x^2+x+1\right)\left(x^6-x^4+x^3-x+1\right)\)
c: \(x^8+x^4+1\)
\(=\left(x^8+2x^4+1\right)-x^4\)
\(=\left(x^4-x^2+1\right)\cdot\left(x^4+x^2+1\right)\)
\(=\left(x^4-x^2+1\right)\left(x^2+1-x\right)\left(x^2+1+x\right)\)
Đúng 2
Bình luận (0)
a)\(x^4+4\\ =\left(x^2\right)^2+4x^2+4-4x^2\\ =\left[\left(x^2\right)^2+4x^2+4\right]-\left(2x\right)^2\\ =\left(x^2+2\right)^2-\left(2x\right)^2\\ =\left(x^2+2+2x\right)\left(x^2+2-2x\right)\)
Đúng 1
Bình luận (0)
\(a)\; x^4+4 \\= x^4+4x^2+4-4x^2\\=(x^2+2)^2-4x^2\\=(x^2+2-2x)(x^2+2+2x)\)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử bằng phương pháp thêm bớt hạng tử:a) 64
x
4
+ 81; b)
x
8
+
4
y
4
; c)
x
8
+
x
7
+1.
Đọc tiếp
Phân tích đa thức thành nhân tử bằng phương pháp thêm bớt hạng tử:
a) 64 x 4 + 81; b) x 8 + 4 y 4 ; c) x 8 + x 7 +1.
Cho hàm số
y
1
4
x
4
-
2
x
+
3
có đồ thị như hình dưới. Tổng tất cả các giá trị nguyên của tham số m để phương trình
x
4
-
8
x
2
+
12
m
có ngh...
Đọc tiếp
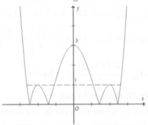
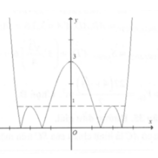
Cho hàm số y = 1 4 x 4 - 2 x + 3 có đồ thị như hình dưới. Tổng tất cả các giá trị nguyên của tham số m để phương trình x 4 - 8 x 2 + 12 = m có nghiệm phân biệt là:
![]()
![]()
![]()
![]()
Cho hàm số
y
1
4
x
4
-
2
x
+
3
có đồ thị như hình dưới. Tổng tất cả các giá trị nguyên của tham số m để phương trình
x
4
-
8
x
2
+
12
m
có ngh...
Đọc tiếp
Cho hàm số y = 1 4 x 4 - 2 x + 3 có đồ thị như hình dưới. Tổng tất cả các giá trị nguyên của tham số m để phương trình x 4 - 8 x 2 + 12 = m có nghiệm phân biệt là:
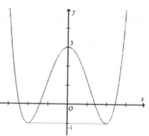
A. 6
B. 10
C. 0
D. 3.
Cho hàm số
y
−
1
4
x
4
+
2
x
2
−
1
có đồ thị (C). Khẳng định nào sau đây sai? A. Đồ thị (C) có trục đối xứng là trục Oy B. Đồ thị (C) không có tiệm cận C. Đồ thị (C) có trục đối xứng là trục Ox D. Đồ thị (C) có 3 điểm cực trị
Đọc tiếp
Cho hàm số y = − 1 4 x 4 + 2 x 2 − 1 có đồ thị (C). Khẳng định nào sau đây sai?
A. Đồ thị (C) có trục đối xứng là trục Oy
B. Đồ thị (C) không có tiệm cận
C. Đồ thị (C) có trục đối xứng là trục Ox
D. Đồ thị (C) có 3 điểm cực trị
Đáp án C
Đồ thị (C) có trục đối xứng là trục Oy.
Đúng 0
Bình luận (0)
Phân tích đa thức
x
8
+
x
4
+ 1 thành nhân tử ta được A.
(
x
4
–
x
2
+
1
)
(
x
2
–
x
+
...
Đọc tiếp
Phân tích đa thức x 8 + x 4 + 1 thành nhân tử ta được
A. ( x 4 – x 2 + 1 ) ( x 2 – x + 1 ) ( x 2 – x – 1 )
B. ( x 4 – x 2 + 1 ) ( x 2 – x + 1 )
C. ( x 4 - x 2 + 1 ) ( x 2 – x + 1 ) ( x 2 + x + 1 )
D. ( x 4 + x 2 + 1 ) ( x 2 – x + 1 ) ( x 2 + x + 1 )
x 8 + x 4 + 1 = x 8 + 2 x 4 + 1 – x 4 = ( x 8 + 2 x 4 + 1 ) – x 4 = [ ( x 4 ) 2 + 2 . x 4 . 1 + 12 ] – x 4 = ( x 4 + 1 ) 2 – ( x 2 ) 2 = ( x 4 + 1 – x 2 ) ( x 4 + 1 + x 2 ) = ( x 4 – x 2 + 1 ) ( x 4 + 2 x 2 – x 2 + 1 ) = ( x 4 – x 2 + 1 ) [ ( ( x 2 ) 2 + 2 . 1 . x 2 + 1 ) – x 2 ] = ( x 4 – x 2 + 1 ) [ ( x 2 + 1 ) 2 – x 2 ] = ( x 4 – x 2 + 1 ) ( x 2 + 1 – x ) ( x 2 + 1 + x ) = ( x 4 – x 2 + 1 ) ( x 2 – x + 1 ) ( x 2 + x + 1 )
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Cho hàm số
y
1
4
x
4
-
2
x
2
+
3
có đồ thị như hình dưới. Tổng tất cả các giá trị nguyên của tham số m để phương trình
x
4...
Đọc tiếp
Cho hàm số y = 1 4 x 4 - 2 x 2 + 3 có đồ thị như hình dưới. Tổng tất cả các giá trị nguyên của tham số m để phương trình x 4 + 8 x 2 + 12 = m có 8 nghiệm phân biệt là:
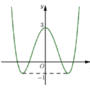
A. 3
B. 10
C. 0
D. 6
Đáp án D
Cách giải: 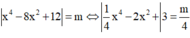
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = 1 4 x 4 - 2 x 2 + 3
và đường thẳng y = m 4
Từ đồ thị hàm số y = 1 4 x 4 - 2 x 2 + 3 ta suy ra đồ thị hàm số y = 1 4 x 4 - 2 x 2 + 3 có hình dạng như sau:
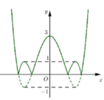
Dựa vào đồ thị hàm số ta thấy để đường thẳng y = m 4 cắt đồ thị hàm số y = 1 4 x 4 - 2 x 2 + 3 tại 8 điểm phân biệt
![]()
Đúng 0
Bình luận (0)
Trong các phát biểu sau khi nói về hàm số
y
1
4
x
4
−
2
x
2
+
1
, phát biểu nào đúng? A. Hàm số có một điểm cực tiểu và hai điểm cực đại. B. Hàm số có một điểm cực đại và hai điểm cực tiểu. C. Hàm số có một điểm cực trị. D. Hàm số có một điểm cực đại và một điểm cực tiểu.
Đọc tiếp
Trong các phát biểu sau khi nói về hàm số y = 1 4 x 4 − 2 x 2 + 1 , phát biểu nào đúng?
A. Hàm số có một điểm cực tiểu và hai điểm cực đại.
B. Hàm số có một điểm cực đại và hai điểm cực tiểu.
C. Hàm số có một điểm cực trị.
D. Hàm số có một điểm cực đại và một điểm cực tiểu.
Trong các phát biểu sau khi nói về hàm số
y
1
4
x
4
−
2
x
2
+
1
, phát biểu nào đúng? A. Hàm số có một điểm cực tiểu và hai điểm cực đại. B. Hàm số có một điểm cực đại và hai điểm cực tiểu. C. Hàm số có một điểm cực trị. D. Hàm số có một điểm cực đại và một điểm cực tiểu.
Đọc tiếp
Trong các phát biểu sau khi nói về hàm số y = 1 4 x 4 − 2 x 2 + 1 , phát biểu nào đúng?
A. Hàm số có một điểm cực tiểu và hai điểm cực đại.
B. Hàm số có một điểm cực đại và hai điểm cực tiểu.
C. Hàm số có một điểm cực trị.
D. Hàm số có một điểm cực đại và một điểm cực tiểu.