Tìm GTNN cûa biêu thuc:
2x2 + 4x - 1
Tìm giá tri nguyên cûa n de giá tru cûa bîêu thuc 3n3 +10n2 -5 chia het cho 3n+1
CÁC BN GIÚP MK BÀI NÀY BÄNG CÁCH LÀM PHÉP CHIA DOC , GIÚP MK VS NHÉ , THANKS
Ta có : \(\frac{3n^3+10n^2-5}{3n+1}=n^2+3n-\frac{6}{3n+1}\)
Để \(3n^3+10n^2-5⋮3n+1\) \(\Leftrightarrow6⋮3n+1\)
\(\Rightarrow3n+1\inƯ\left(6\right)=\left\{-6;-3;-2;-1;1;2;3;6\right\}\)
\(\Rightarrow3n=\left\{-7;-4;-3;-2;0;1;2;5\right\}\)
\(\Rightarrow n=\left\{-\frac{7}{3};-\frac{4}{3};-1;-\frac{2}{3};0;\frac{1}{3};\frac{2}{3};\frac{5}{3}\right\}\)
Mà n là số nguyên nên \(n=\left\{-1;0\right\}\)
tìm GTNN cûa 2016+|x-3|+|y-5|
Ta có |x- 3|>= 0 với mọi x
|y- 5|>=0 với mọi y
=> |x- 3| + |y- 5| với mọi x,y
=> 2016+ |x- 3|+ |y- 5| >= 2016 với mọi x,y
Dấu = xảy ra <=> x- 3= 0 <=> x= 3
y- 5= 0 y= 5
Vậy GTNN của 2016+ |x- 3|+ |y- 5| là 2016 tại x= 3 và y= 5
Tìm GTNN GTLN của biểu thức
M = 2x2 + 5y - 4x√y - 4x - 8√y + 2036
tìm gtnn (gtln) của:
a) A= 4x2-4x+10 b) B= 2x2-3x-1
c) C= 4x2+2y2+4xy+4x+6y+1 d) D= (3x-1)2-4(3x-1)x+4x2
e) G= 9x2+2y2+6xy+4y+5 f) H= 2x2+3y2-2xy+4y+2x+5
g) K= xy+yz+zx; biết x+y+z= 3
nhờ mn giúp mik vs nha
\(A=\left(2x-1\right)^2+9\ge9\\ A_{min}=9\Leftrightarrow x=\dfrac{1}{2}\\ B=2\left(x^2-2\cdot\dfrac{3}{4}x+\dfrac{9}{16}\right)+\dfrac{1}{8}=2\left(x-\dfrac{3}{4}\right)^2+\dfrac{1}{8}\ge\dfrac{1}{8}\\ B_{min}=\dfrac{1}{8}\Leftrightarrow x=\dfrac{3}{4}\\ C=\left(4x^2+4xy+y^2\right)+2\left(2x+y\right)+1+\left(y^2+4y+4\right)-4\\ C=\left[\left(2x+y\right)^2+2\left(2x+y\right)+1\right]+\left(y+2\right)^2-4\\ C=\left(2x+y+1\right)^2+\left(y+2\right)^2-4\ge-4\\ C_{min}=-4\Leftrightarrow\left\{{}\begin{matrix}2x=-1-y\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=-2\end{matrix}\right.\)
\(D=\left(3x-1-2x\right)^2=\left(x-1\right)^2\ge0\\ D_{min}=0\Leftrightarrow x=1\\ G=\left(9x^2+6xy+y^2\right)+\left(y^2+4y+4\right)+1\\ G=\left(3x+y\right)^2+\left(y+2\right)^2+1\ge1\\ G_{min}=1\Leftrightarrow\left\{{}\begin{matrix}3x=-y\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-2\end{matrix}\right.\)
\(H=\left(x^2-2xy+y^2\right)+\left(x^2+2x+1\right)+\left(2y^2+4y+2\right)+2\\ H=\left(x-y\right)^2+\left(x+1\right)^2+2\left(y+1\right)^2+2\ge2\\ H_{min}=2\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=-1\\y=-1\end{matrix}\right.\Leftrightarrow x=y=-1\)
Ta luôn có \(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)
\(\Leftrightarrow2x^2+2y^2+2z^2-2xy-2yz-2xz\ge0\\ \Leftrightarrow x^2+y^2+z^2\ge xy+yz+xz\\ \Leftrightarrow x^2+y^2+z^2+2xy+2yz+2xz\ge3xy+3yz+3xz\\ \Leftrightarrow\left(x+y+z\right)^2\ge3\left(xy+yz+xz\right)\\ \Leftrightarrow\dfrac{3^2}{3}\ge xy+yz+xz\\ \Leftrightarrow K\le3\\ K_{max}=3\Leftrightarrow x=y=z=1\)
tìm GTNN của biểu thức A= 2x2-8x+1
Tìm GTLN của B = -5x2-4x+1
cảm ơn nha^^
a: Ta có: \(A=2x^2-8x+1\)
\(=2\left(x^2-4x+\dfrac{1}{2}\right)\)
\(=2\left(x^2-4x+4-\dfrac{7}{2}\right)\)
\(=2\left(x-2\right)^2-7\ge-7\forall x\)
Dấu '=' xảy ra khi x=2
Tìm GTLN (max), GTNN (min) của hàm số y = x 3 - 2 x 2 - 4 x + 8 khi x ∈ - 1 ; 1
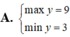
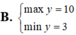
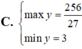
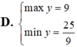
1)Tìm GTNN của bt:
a) A=x2(x-1)2+2x2-4x-1
b) B=(x-5)(x-3)(x+2)(x+4)+2022
2)
a) Phân tích đa thức thành nhân tử
x3-2x2+26x-24
b) Với n là số nguyên . CMR: 7n3-9n2+26n-12
2.a) (ko phân tích được, bạn coi lại nhé)
b) phần còn lại của chứng minh là gì thế bạn?
1)Tìm GTNN của bt:
a) A=x2(x-1)2+2x2-4x-1
b) B=(x-5)(x-3)(x+2)(x+4)+2022
2)
a) Phân tích đa thức thành nhân tử
x3-2x2+26x-24
b) Với n là số nguyên . CMR: 7n3-9n2+26n-12 chia hết cho 6
1)Tìm GTNN của bt:
a) A=x2(x-1)2+2x2-4x-1
b) B=(x-5)(x-3)(x+2)(x+4)+2022
2)
a) Phân tích đa thức thành nhân tử
x3-2x2+26x-24
b) Với n là số nguyên . CMR: 7n3-9n2+26n-12 chia hết cho 6
1)Tìm GTNN của bt:
a) A=x2(x-1)2+2x2-4x-1
b) B=(x-5)(x-3)(x+2)(x+4)+2022
2)
a) Phân tích đa thức thành nhân tử
x3-2x2+26x-24
b) Với n là số nguyên . CMR: 7n3-9n2+26n-12 chia hết cho 6