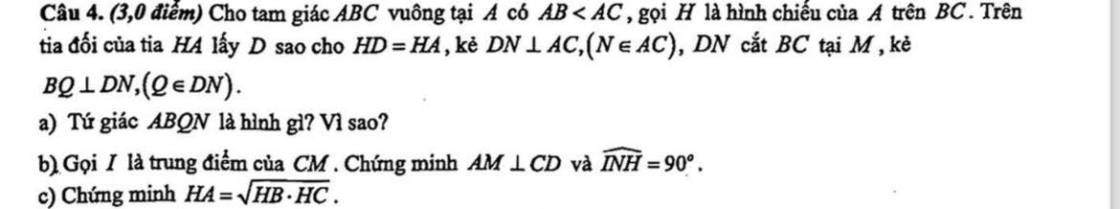Giải giúp câu câu c thôi ạ. Xin cảm ơn
NT
Những câu hỏi liên quan
Giải giúp mình câu d thôi ạ. Xin cảm ơn 
a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình của ΔABC
Suy ra: EF//BC và \(EF=\dfrac{BC}{2}\)
hay \(EF=\dfrac{7.2}{2}=3.6\left(cm\right)\)
b: Xét tứ giác ADCE có
F là trung điểm của đường chéo AC
F là trung điểm của đường chéo ED
Do đó: ADCE là hình bình hành
Suy ra: AE=CD
mà AE=BE
nên CD=BE
Đúng 0
Bình luận (0)
Mn giúp em làm bài hình này câu c d thôi ạ đc không ạ?:)
E xin cảm ơn

 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
Giải giúp e câu c với ạ. Xin cảm ơn
giải giúp em câu C thôi ạ, em cảm ơn nhiều lắm ạ. M = \(\dfrac{3}{\sqrt{x}+3}\)
c) A = x.M + (4x + 7)/(√x + 3)
= 3x/(√x + 3) + (4x + 7)/(√x + 3)
= (7x + 7)/(√x + 3)
Để A nhỏ nhất thì 7x + 7 nhỏ nhất
Mà x ≥ 0
⇒ 7x + 7 ≥ 7
⇒ GTNN của A là 7/3 khi x = 0
Đúng 1
Bình luận (0)
Giải giúp mình câu c với ạ. Xin cảm ơn rất nhiều.
Giải giúp em câu b với, câu b thôi nha. Em cảm ơn nhiều ạ! 
Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:
\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)
Gọi \(d_1\) là ảnh của d qua phép đối xứng trục
Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:
\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)
Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d
Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:
\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)
Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'
\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)
\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)
Đúng 2
Bình luận (1)
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ
a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)
Đúng 1
Bình luận (3)
Mọi người giúp e với giải giúp em câu 2 và câu 3 ạ em xin cảm ơn