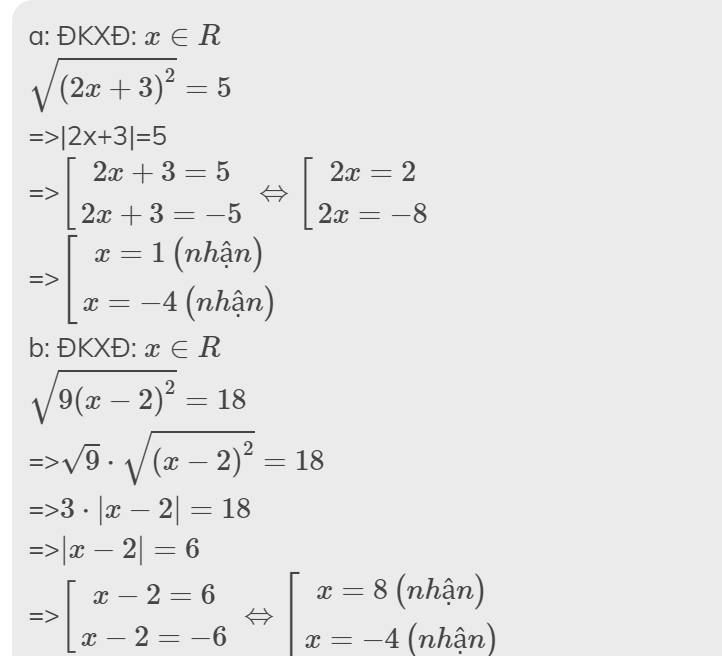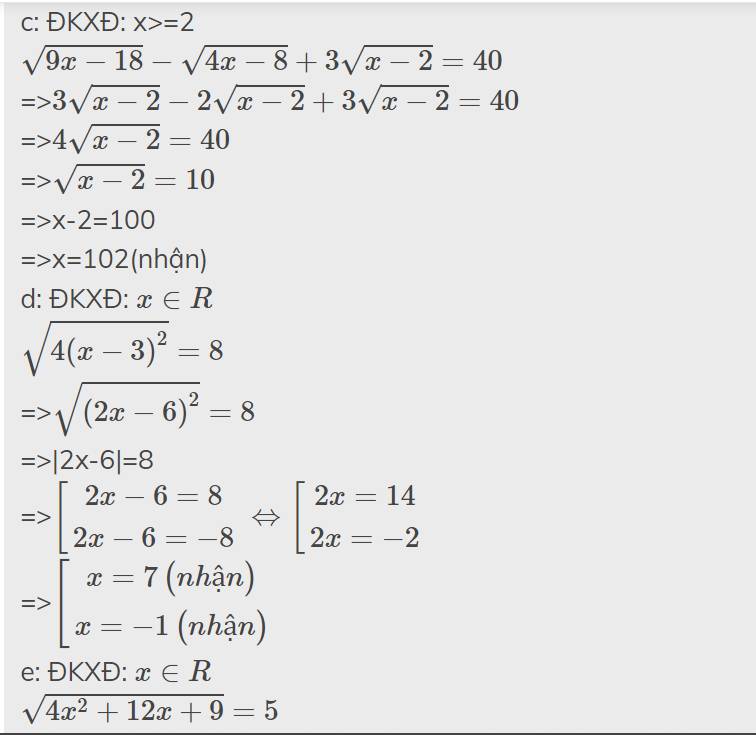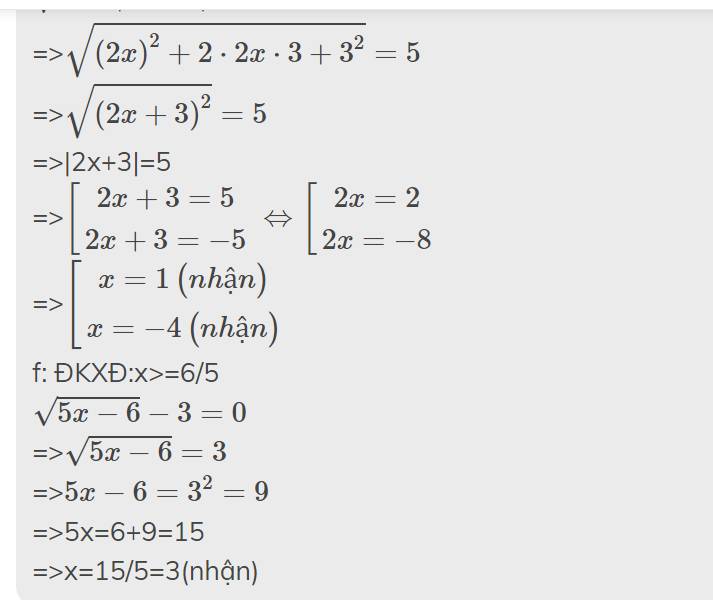Giải phương trình: \(\left(x+3\sqrt{x}+2\right)\left(x+9\sqrt{x}+18\right)=168x\)
TT
Những câu hỏi liên quan
giải phương trình \(\left(x+3\sqrt{x}+2\right)\left(x+9\sqrt{x}+18\right)=168x\)
Giair phương trình:1) sqrt[5]{32-x^2}-sqrt[5]{1-x^2}42) sqrt{x}+sqrt[4]{20-x}43) x^3+12sqrt{3x-1}4) sqrt[3]{x-1}+3sqrt[4]{82-x}5) a.left(x+3sqrt{x}+2right)left(x+9sqrt{x}+18right)168xb.sqrt{5x^2+14x+9}-sqrt{x^2-x-20}5sqrt{x+1}
Đọc tiếp
Giair phương trình:
1) \(\sqrt[5]{32-x^2}-\sqrt[5]{1-x^2}=4\)
2) \(\sqrt{x}+\sqrt[4]{20-x}=4\)
3) \(x^3+1=2\sqrt{3x-1}\)
4) \(\sqrt[3]{x-1}+3=\sqrt[4]{82-x}\)
5)
\(a.\left(x+3\sqrt{x}+2\right)\left(x+9\sqrt{x}+18\right)=168x\)
\(b.\sqrt{5x^2+14x+9}-\sqrt{x^2-x-20}=5\sqrt{x+1}\)
a) ĐKXĐ: \(x\ge0\)
Ta có: \(\left(x+3\sqrt{x}+2\right)\left(x+9\sqrt{x}+18\right)=168x\)
\(\Leftrightarrow\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)\left(\sqrt{x}+6\right)=168x\)
\(\Leftrightarrow\left(x+6\right)^2+12\sqrt{x}\left(x+6\right)-133=0\)
\(\Leftrightarrow\left(x+6\right)^2+19\sqrt{x}\left(x+6\right)-7\sqrt{x}\left(x+6\right)-133=0\)
\(\Leftrightarrow\left(x+6\right)\left(x+19\sqrt{x}+6\right)-7\sqrt{x}\left(x+19\sqrt{x}+6\right)=0\)
\(\Leftrightarrow\left(x-7\sqrt{x}+6\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left(\sqrt{x}-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=36\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Giải Phương Trình
\(\sqrt{\left(2x+3\right)^2}=5\)
\(\sqrt{9\left(x-2\right)^2}=18\)
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
\(\sqrt{4.\left(x-3\right)^2}=8\)
\(\sqrt{5x-6}-3=0\)
giải phương trình :
\(9\left(\sqrt{x+1}+\sqrt{x-2}\right)+1=4\left(\sqrt{\left(x+1\right)^3}-\sqrt{\left(x-2\right)^3}\right)\)
Giải phương trình sau : \(x^2-x-18+\left(2x+9\right)\sqrt{x+3}-2\sqrt{5x-1}=0\)
Giải phương trình :
\(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)=168x^2\)
Dễ thấy \(x=0\) không là nghiệm của phương trình. Ta có "
\(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)=168x^2\Leftrightarrow\left(x^2+7x+6\right)\left(x^2+5x+6\right)=168x^2\)
\(\Leftrightarrow\left(x+\frac{6}{x}+7\right)\left(x+\frac{6}{x}+5\right)=168\)
Đặt \(t=x+\frac{6}{x}\) ta được :
\(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)=168x^2\Leftrightarrow\left(t+7\right)\left(t+5\right)=168\)
\(\Leftrightarrow t^2+12t-133=0\Leftrightarrow\left[\begin{array}{nghiempt}t=7\\t=-19\end{array}\right.\)
Do vậy :
\(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)=168x^2\Leftrightarrow\begin{cases}x+\frac{6}{x}=7\\x+\frac{6}{x}=-19\end{cases}\)
\(\Leftrightarrow\begin{cases}x^2-7x+6=0\\x^2+19x+6=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=1\\x=6\\x=\frac{-19\pm\sqrt{337}}{2}\end{cases}\)
Vậy phương trình đã cho có tập nghiệm :
\(\left\{1;6;\frac{-19-\sqrt{337}}{2};\frac{-19+\sqrt{337}}{2}\right\}\)
Đúng 0
Bình luận (0)
\(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)=168x^2\)
<=>\(\left(x+1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)=168x^2\)
<=>\(\left(x^2+7x+6\right)\left(x^2+5x+6\right)=168x^2\)(1)
Đặt t=x2+5x+6
PT (1) trở thành: (t+2x)t=168x2
<=>t2+2tx-168x2=0
<=>t2-12tx+14tx-168x2=0
<=>t.(t-12x)+14x.(t-12x)=0
<=>(t-12x)(t+14x)=0
<=>t-12x=0 hoặc t+14x=0
*t-12x=0 (thích giải denta cũng được)
<=>x2-7x+6=0
<=>x2-x-6x+6=0
<=>x.(x-1)-6.(x-1)=0
<=>(x-1)(x-6)=0
<=>x=1 hoặc x=6
*t+14x=0
<=>x2+19x+6=0
Giải denta là vừa tại số lớn lắm tự làm típ ..............
Đúng 0
Bình luận (0)
1.a, Giải phương trình \(\left(\sqrt{x 3}-\sqrt{x 1}\right)\left(x^2 \sqrt{x^2 4x 3}\right)=2x\)b, Giải hệ phương trình \(\left\{{}\begin{matrix}x^2\left(y^2 1\right) 2y\left(x^2 x 1\right)=3\\\left(x^2 x\right)\left(y^2 y\right)=1\end{matrix}\right....
Xem chi tiết
giải phương trình :
a, \(\left(x+9\right)\left(2-\sqrt{9+2x}\right)^2=2x^2\)
b,\(\left(2x+10\right)\left(1-\sqrt{3+2x}\right)^2=4\left(x+1\right)^2\)
a. Đề bài sai, phương trình không giải được
b.
ĐKXĐ: \(x\ge-\dfrac{2}{3}\)
\(\left(2x+10\right)\left(\dfrac{1-\left(3+2x\right)}{1+\sqrt{3+2x}}\right)^2=4\left(x+1\right)^2\)
\(\Leftrightarrow\dfrac{\left(2x+10\right)4.\left(x+1\right)^2}{\left(1+\sqrt{3+2x}\right)^2}=4\left(x+1\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}4\left(x+1\right)^2=0\Rightarrow x=-1\\2x+10=\left(1+\sqrt{3+2x}\right)^2\left(1\right)\end{matrix}\right.\)
Xét (1)
\(\Leftrightarrow2x+10=2x+4+2\sqrt{2x+3}\)
\(\Leftrightarrow\sqrt{2x+3}=3\)
\(\Leftrightarrow x=3\)
Đúng 1
Bình luận (2)
Giải phương trình
\(13\sqrt{5-x}+18\sqrt{x+8}=61+x+3\sqrt{\left(5-x\right)\left(x+8\right)}\)
mn giúp em vs ạ