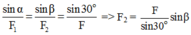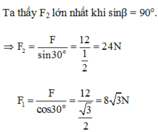Tính các giá trị của s khi cho t lần lượt lấy các giá trị 1h; 2h; 3h; 4h;... rồi giải thích tại sao s là hàm số của t
Help Me![]()
![]()
![]()
Bài 1: Cho hàm số y = f(x) = 5 - 2x
a) Tính f(-2); f(-1)
b) Tính các giá trị của x ứng với các giá trị của y lần lượt là 5; 3; -1
Bài 2: Tìm tập xác định của các hàm số sau:
a) y = x3 - 2x2 + x -1
b) y = \(\sqrt{2x-1}\)
c) y = \(\frac{x-1}{\left(x+1\right)\left(x-3\right)}\)
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) = x 3 - 3 x 2 trên đoạn [-1;1]. Tính M + m.
A. -4
B. 4
C. -2
D. 2
Gọi M mà m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = 1 - x - 2 x 2 x + 1 . Khi đó giá trị của M-m là:
A. -2
B. -1
C. 1
D. 2
Điền Đ (đúng) hoặc S (sai) trong các phát biểu sau:
| Các phát biểu | Đ/S |
| a) Nếu tổng hai số tự nhiên bằng 0 thì cả hai số tự nhiên đó đều bằng 0. | |
| b) Nếu tổng hai số nguyên bằng 0 thì cả hai số nguyên đó đều bằng 0. | |
| c) Tổng của nhiều số nguyên âm cũng là một số nguyên âm có giá trị tuyệt đối bằng tổng các giá trị tuyệt đối của các số đó. | |
| d) Giá trị tuyệt đối của tổng nhiều số nguyên bằng tổng các giá trị tuyệt đối của các số đó. |
a) Đ
b) S
Vì tổng của hai số nguyên bằng 0 thì cả hai số nguyên đó đều bằng 0 hoặc hai số đó là hai số đối nhau. Ví dụ: (-3) + 3 = 0+ 0 = 0
c) Đ
d) S
Vì khẳng định sẽ bị sai khi các số nguyên đó không cùng dấu.
viết công thức và cho biết các chức năng của: hàm tính tổng, hàm tính trung bình cộng,hàm xác định giá trị lớn nhất, hàm xác định giá trị nhỏ nhất
Công thức của hàm tính tổng =Sum(a,b,c,...)
Công thức của hàm tính trung bình cộng : =AVERAGE(a,b,c,....)
Công thức của hàm xác định giá trị lớn nhất : =MAX(a,b,c,......)
Công thức của hàm xác định giá trị nhỏ nhất : =MIN(a,b,c,....)
Chức năng của hàm tính tổng : Tính tổng của một dãy số
Chức năng của hàm tính trung bình cộng : Tính trung bình của một dãy số
Chức năng của hàm xác định giá trị lớn nhất : Xác định giá trị lớn nhất
Chức năng của hàm xác định giá trị nhỏ nhất : Xác định giá trị nhỏ nhất
Cho x và y là 2 đại lượng tỉ lệ nghịch với nhau khi x nhận các giá trị x1=3 , x2=2 thì tổng các giá trị tương ứng của y là 15
a , Hãy biểu diễn y theo z
b , Tìm giá trị của x khi y=23
a: Vì x và y tỉ lệ nghịch nên \(x_1y_1=x_2y_2\)
=>\(3y_1=2y_2\)
hay \(\dfrac{y_1}{2}=\dfrac{y_2}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được;
\(\dfrac{y_1}{2}=\dfrac{y_2}{3}=\dfrac{y_1+y_2}{2+3}=\dfrac{15}{5}=3\)
Do đó: \(y_1=6\)
\(k=x_1\cdot y_1=3\cdot6=18\)
=>y=18/x
b: Khi y=23 thì 18/x=23
hay x=18/23
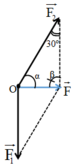
Một lực có độ lớn 12 N được phân tích thành hai lực F 1 ⇀ và F 2 ⇀ . Biết các lực tạo với nhau một góc là: ( F 1 ⇀ , F 2 ⇀ )= 150° và F 2 có giá trị lớn nhất. Độ lớn của các lực F 1 ⇀ và F 2 ⇀ lần lượt là
A. 8 3 N và 24N
B. 8 3 N và 4 3 N
C. 4 3 N và
D. 4 3 N và 24N
Chọn A.
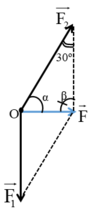
Hợp lực có độ lớn 12N (Hình vẽ). Theo định lí hàm số sin:
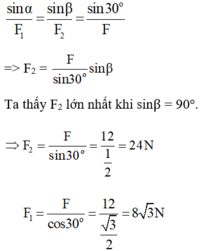
Cho hàm số y=2x. Biết y1 và y2 là các giá trị của hàm số tương ứng với các giá trị của biến số x1, x2 và x1x2 =5, y1=7. Khi đó y2=...?
Một lực có độ lớn 12 N được phân tích thành hai lực F 1 → và F 2 → . Biết các lực tạo với nhau một góc là: F 1 → , F 2 → = 150 và F 2 có giá trị lớn nhất. Độ lớn của các lực F 1 → và F 2 → lần lượt là
A. 8 3 N v à 24 N
B. 8 3 N v à 4 3 N
C. 4 3 N v à 8 3 N
D. 4 3 N v à 24 N
Chọn A.
Hợp lực có độ lớn 12N (Hình vẽ). Theo định lí hàm số sin