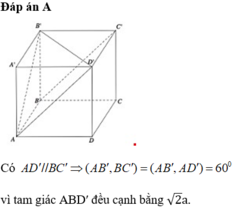
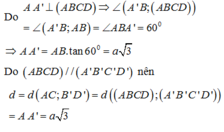Chohìnhlập phương.ABCD A B C D′′′′. Góc giữa hai đường thẳngAC′′vàBDbằng
NH
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A vài một điểm D nằm giữ A và B.Đường tròn đường kính BD cắt BC tại E;các đường thẳng CD,AElần lượt cắt đường tròn tại điểm thứ hai F;G.Chứng minh:
a)Tam giác ABC đồng dạng tam giác BDE
b)tứ giác ADEC và AFBC nội tiếp được trong một đường tròn
c)AC song song FG
d) Các đường thẳngAC,DE,BF đồng quy
Trên đường thẳng d ta có các điểm A, B, C, D sao cho điểm C ở giữa hai điểm A và B, điểm D ở giữa hai điểm A và C. Điểm O là một điểm nằm ngoài đường thẳng d biết rằng góc AOD = 30độ, góc DOC = 40độ, góc AOB = 90độ. Tính góc AOC; góc COB.
Các bạn giúp mk bài này với, mình đang cần gấp các bạn nhé!
Ai nhanh tay mk tick cho nào!
Trong mặt phẳng cho hai đường thẳng a, b.a) Nếu a và b cắt nhau tại O (Hình 2) thì góc giữa hai đường thẳng a, b được xác định như thế nào?b) Nếu a // b thì góc giữa a và b bằng bao nhiêu độ?c) Nếu a và b trùng nhau thì góc giữa a và b bằng bao nhiêu độ?
Đọc tiếp
Trong mặt phẳng cho hai đường thẳng a, b.
a) Nếu a và b cắt nhau tại O (Hình 2) thì góc giữa hai đường thẳng a, b được xác định như thế nào?
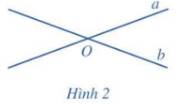
b) Nếu a // b thì góc giữa a và b bằng bao nhiêu độ?
c) Nếu a và b trùng nhau thì góc giữa a và b bằng bao nhiêu độ?
a) Nếu a và b cắt nhau tại O thì: \(0^\circ \le \left( {a,b} \right) \le 90^\circ \)
b) Nếu a // b thì không có góc tạo bởi a và b
c) Nếu a và b trùng nhau thì góc giữa a và b bằng \(0^\circ \)
Đúng 0
Bình luận (0)
1)Vẽ hình theo yêu cầu sau: Cho đường thẳng a và 3 điểm A,B,C thuộc đường thẳng a (điểm B nằm giữa hai điểm A và C). Trên hai nửa mặt phẳng có bờ là đường thẳng a lấy hai điểm D và E. Gọi I là giao điểm của đường thẳng a với đoạn thẳng DE. Vẽ đoạn thẳng BD, BE. 2)Dựa vào hình vẽ ở câu a. Hãy trả lời các câu hỏi sau: a) Kể tên hai nửa mặt phẳng đối nhau bờ là đường thẳng AC. b) Kể tên các góc bẹt. c) Gọi tên hai tia đối nhau. d) Tia BD nằm giữa hai tia nào? e) Tia BE nằm giữa hai tia nào? f) Tia...
Đọc tiếp
1)Vẽ hình theo yêu cầu sau: Cho đường thẳng a và 3 điểm A,B,C thuộc đường thẳng a (điểm B nằm giữa hai điểm A và C). Trên hai nửa mặt phẳng có bờ là đường thẳng a lấy hai điểm D và E. Gọi I là giao điểm của đường thẳng a với đoạn thẳng DE. Vẽ đoạn thẳng BD, BE. 2)Dựa vào hình vẽ ở câu a. Hãy trả lời các câu hỏi sau: a) Kể tên hai nửa mặt phẳng đối nhau bờ là đường thẳng AC. b) Kể tên các góc bẹt. c) Gọi tên hai tia đối nhau. d) Tia BD nằm giữa hai tia nào? e) Tia BE nằm giữa hai tia nào? f) Tia BC nằm giữa hai tia nào?
giúp mình với
Cho hình lăng trụ đứng ABCD. D có ABCD là hình thoi cạnh a, góc giữa đường thẳng A B và mặt phẳng (ABCD) bằng 600 . Tính khoảng cách d giữa hai đường thẳng AC và B D
Đọc tiếp
Cho hình lăng trụ đứng ABCD. 'D ' có ABCD là hình thoi cạnh a, góc giữa đường thẳng A 'B và mặt phẳng (ABCD) bằng 600 . Tính khoảng cách d giữa hai đường thẳng AC và B ' D '
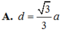
![]()
![]()
Cho hình lập phương ABCD.A'B'C'D'. Tính góc giữa hai đường thẳng AB' và A'C'.
A. 600
B. 300
C. 450
D. 900
\(A'C'||AC\Rightarrow\) góc cần tìm là góc \(\widehat{CAB'}\)
Mặt khác \(AB'=AC=B'C\) (các đường chéo của hình vuông bằng nhau)
\(\Rightarrow\Delta AB'C\) đều
\(\Rightarrow\widehat{CAB'}=60^0\)
Đúng 2
Bình luận (0)
Cho hình lập phương ABCD.A'B'C'D'. Tính góc giữa hai đường thẳng AB' và A'C'.
A. 600
B. 300
C. 450
D. 900
1) Cho đoạn thẳngAC và BD cắt nhau ở trung điểm O của mỗi đoạn :
a) AD = BC ; AB = DC
b) CDA = CBA, BAD = BCD
2) Cho tam giác ABC có A = 90 độ. Gọi I là giao điểm của hai phân giác xuất phát từ đỉnh B và C. Tính số đo góc BIC.
Cm: a) Xét t/giác OAD và t/giác OCB
có: OA = OC (gt)
\(\widehat{AOD}=\widehat{COB}\) (đối đỉnh)
OD = OB (gt)
=> t/giác OAD = t/giác OCD (c.g.c)
=> AD = BC (2 cạnh t/ứng)
Tương tự, xét t/giác AOB và t/giác COD
có: OA = OC (gt)
\(\widehat{AOB}=\widehat{COD}\) (Đối đỉnh)
OB = OD (gt)
=> t/giác AOB = t/giác COD (c.g.c)
=> AB = DC (2 cạnh t/ứng)
b) Xét t/giác ADC và t/giác CAB
có: AC : chung
AD = BC (cmt)
AB = DC (cmt)
=> t/giác ADC = t/giác CAB (c.c.c)
=> \(\widehat{CDA}=\widehat{CBA}\)(2 góc t/ứng)
Xét t/giác ADB và t/giác CBD
có: AB = CD (cmt)
AD = CB (cmt)
BD : chung
=> t/giác ADB = t/giác CBD (c.c.c)
=> \(\widehat{BAD}=\widehat{BCD}\)(2 góc t/ứng)
Đúng 0
Bình luận (0)
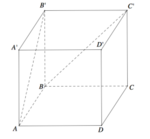
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên).
A. 60 °
B. 90 °
C. 45 °
D. 300 °