Cm 2x-2x2-1<0 với mọi số thực x
TT
Những câu hỏi liên quan
CM các bất phương trình sau luôn dương vs mọi x
1)2x2-2x+17>0
2)-x2+6x-18<0
3)|x-1|+|x|+2>1
BPT thì làm sao gọi là luôn dương hả bạn? Đề phải là CMR các BPT sau luôn đúng với mọi $x$.
1.
Ta có: $2x^2-2x+17=x^2+(x^2-2x+1)+16=x^2+(x-1)^2+16\geq 16>0$ với mọi $x\in\mathbb{R}$
Do đó BPT luôn đúng với mọi $x$
2.
$-x^2+6x-18=-(x^2-6x+18)=-[(x^2-6x+9)+9]=-[(x-3)^2+9]$
$=-9-(x-3)^2\leq -9<0$ với mọi $x\in\mathbb{R}$
Vậy BPT luôn đúng với mọi $x$
3.
$|x-1|+|x|+2\geq 0+0+2=2>1$ với mọi $x\in\mathbb{R}$
Do đó BPT luôn đúng với mọi $x$
Đúng 0
Bình luận (0)
Tìm phân thức A thỏa mãn đẳng thức sau:
A
+
6
x
2
−
1
3
x
+
2
x
2
−
2
x
+
1
−
3...
Đọc tiếp
Tìm phân thức A thỏa mãn đẳng thức sau: A + 6 x 2 − 1 = 3 x + 2 x 2 − 2 x + 1 − 3 x − 2 x 2 + 2 x + 1 với x ≠ ± 1 .
Tìm được A = 10 ( x 2 + 1 ) ( x 2 − 1 ) 2
Đúng 0
Bình luận (0)
Thực hiện phép tính:
a)2x(3x2 - 5x + 3) b)-2x2(x2 + 5x - 3) c)-1/2x2(2x3 - 4x + 3)
d) (2x - 1)(x2 +5- 4) c) 7x(x - 4) - (7x + 3)(2x2 - x + 4).
a: \(=6x^3-10x^2+6x\)
b: \(=-2x^4-10x^3+6x^2\)
c: \(=-x^5+2x^3-\dfrac{3}{2}x^2\)
d: \(=2x^3+10x^2-8x-x^2-5x+4=2x^3+9x^2-13x+4\)
Đúng 0
Bình luận (0)
Giải thích vì sao cặp bất phương trình sau tương đương? 2x2 + 5 ≤ 2x - 1 và 2x2 - 2x + 6 ≤ 0
Ta có:
2x2 + 5 ≤ 2x – 1
⇔ 2x2 + 5 + 1 – 2x ≤ 2x – 1 + 1 – 2x (Cộng cả hai vế của BPT với 1 – 2x).
⇔ 2x2 – 2x + 6 ≤ 0.
Vậy hai BPT đã cho tương đương: 2x2 + 5 ≤ 2x – 1 ⇔ 2x2 – 2x + 6 ≤ 0.
Đúng 0
Bình luận (0)
Số nghiệm của phương trình
2
x
2
-
2
x
2
-
3
x
2
-
2
x
+
1
0
là A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Số nghiệm của phương trình 2 x 2 - 2 x 2 - 3 x 2 - 2 x + 1 = 0 là
A. 1
B. 2
C. 3
D. 4
Đặt t = x2 – 2x. Khi đó, phương trình đã cho trở thành:
2t2 – 3t + 1 = 0 ⇔ [ t = 1 t = 1 2
* Với t= 1 thì x2 – 2x = 1 hay x2 – 2x – 1 =0 có ac < 0 nên phương trình này có 2 nghiệm.
* Với t = 1 2 thì x 2 - 2 x = 1 2 ⇔ x 2 - 2 x - 1 2 = 0 có ac < 0 nên phương trình này có 2 nghiệm.
Do đó, phương trình đã cho có 4 nghiệm.
Chọn D.
Đúng 0
Bình luận (0)
x4 – 2x3 + 2x – 1
a3 – a4 + 2a3 + 2a2
x4 + x3 + 2x2 + x + 1
x4 + 2x3 + 2x2 + 2x + 1
x2y + xy2 + x2z + y2z + 2xyz
x3 + x4 + x3 + x2 + x + 1
a: Ta có: \(x^4-2x^3+2x-1\)
\(=\left(x-1\right)\left(x+1\right)\left(x^2+1\right)-2x\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)\left(x+1\right)\cdot\left(x^2-2x+1\right)\)
\(=\left(x-1\right)^3\cdot\left(x+1\right)\)
b: Ta có: \(-a^4+a^3+2a^3+2a^2\)
\(=-a^2\left(a^2-a-2a-2\right)\)
c: Ta có: \(x^4+x^3+2x^2+x+1\)
\(=x^4+x^3+x^2+x^2+x+1\)
\(=\left(x^2+x+1\right)\left(x^2+1\right)\)
Đúng 1
Bình luận (0)
Giải phương trình bằng cách đặt ẩn phụ:
2 x 2 - 2 x 2 + 3 x 2 - 2 x + 1 = 0
2(x2 – 2x)2 + 3(x2 – 2x) + 1 = 0 (1)
Đặt x2 – 2x = t,
(1) trở thành : 2t2 + 3t + 1 = 0 (2).
Giải (2) :
Có a = 2 ; b = 3 ; c = 1
⇒ a – b + c = 0
⇒ (2) có nghiệm t1 = -1; t2 = -c/a = -1/2.
+ Với t = -1 ⇒ x2 – 2x = -1 ⇔ x2 – 2x + 1 = 0 ⇔ (x – 1)2 = 0 ⇔ x = 1.
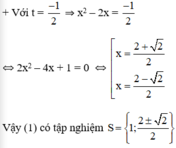
Đúng 0
Bình luận (0)
Bài 9.Rút gọn biểu thức
a)-5x2+3x.(x+2)
b)-2x.(1-x2)-2x3
c)4x.(x-1)-4(x2+2x-1)
d)6x3-2x2(-x2-3x)
e)3x(x-1)-(1+2x).5x
f)-5x2-(x-6).(-2x2)
Giúp mình với mn
\(a\\ -5x^2+3x.\left(x+2\right)=-5x^2+3x^2+6x=-2x^2+6x\\ b\\ -2x.\left(1-x^2\right)-2x^3=-2x+2x^3-2x^3=-2x\\ c\\ 4x.\left(x-1\right)-4.\left(x^2+2x-1\right)\\ =4x^2-4x-4x^2-8x+4=-12x+4\)
Đúng 1
Bình luận (0)
\(d\\ 6x^3-2x^2.\left(-x^2-3x\right)=6x^3+2x^4+6x^3=2x^4+12x^3\\ e\\ 3x.\left(x-1\right)-\left(1+2x\right).5x\\ =3x^2-3x-5x-10x^2=-7x^2-8x\\ f\\ -5x^2-\left(x-6\right).\left(-2x^2\right)=-5x^2+2x^3-12x^2=2x^3-17x^2\)
Đúng 1
Bình luận (0)
Bài 2: Hai phân thức sau có bằng nhau không ?
a)x3-x2/x3-2x2+x và x/x-1
b)x2+2x+1/2x2-2 và x+1/2x-2
a) `(x^3-x^2)/(x^3-2x^2+x)`
`=(x^2(x-1))/(x(x-1)(x-1))`
`=x/(x-1)`
`=>` 2 phân thức bằng nhau.
b) `(x^2+2x+1)/(2x^2-2)`
`=((x+1)(x+1))/(2(x+1)(x-1))`
`=(x+1)/(2(x-1))`
`=(x+1)/(2x-2)`
`=>` 2 phân thức bằng nhau
Đúng 1
Bình luận (0)
a) Ta có: \(\dfrac{x^3-x^2}{x^3-2x^2+x}\)
\(=\dfrac{x^2\left(x-1\right)}{x\left(x^2-2x+1\right)}\)
\(=\dfrac{x\cdot\left(x-1\right)}{\left(x-1\right)^2}=\dfrac{x}{x-1}\)
b) Ta có: \(\dfrac{x^2+2x+1}{2x^2-2}\)
\(=\dfrac{\left(x+1\right)^2}{2\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{x+1}{2x-2}\)
Đúng 0
Bình luận (0)
Kết quả phép tính nhân (2x+1).(x-3) là:
A.2x2+7x-3
B.2x2-5x-3
C.2x2-3
D.x2-5x-2
\(=2x.x-2x.3+x-3\\ =2x^2-6x+x-3\\ =2x^2-5x-3\)
=> Chọn B
Đúng 0
Bình luận (0)




