cho hbh ABCD. các tia p/giác của các góc A, B, C, D cắt nhau như trên h.91. c/m EFGH là hcn

Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
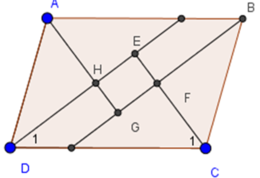
Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
cho hình bình hành ABCD ,AB=6cm,AD=4cm .các tia phân giác của các góc cắt nhau tại các điểm E,F,G,H
a,tứ giác EFGH là hình j vì sao
b,Tính độ dài đoạn EG và FH
c,Hbh ABCD có thêm điều kiện j thì tứ giác EFGH có S lớn nhất
Cho HBH ABCD , các tia phân giác của góc A,B,C,D cắt nhau tại E,F,G,H . CMR tứ giác EFGH là HCN
Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau nhau. Chứng minh EFGH là hình chữ nhật.
Bạn làm xong rồi gửi cho mk, mk giải cho
Ta có: ABCD là hình bình hành ( gt )
\(\Rightarrow\widehat{DAB}=\widehat{DCB};\widehat{ADC}=\widehat{ABC}\)
Dùng định lý tổng 4 góc trong tứ giác ABCD ta có:
\(\widehat{DAB}+\widehat{DCB}+\widehat{ADC}+\widehat{ABC}=360^0\)
Từ 2 điều trên suy ra \(\widehat{DAB}+\widehat{ABC}=\frac{360^0}{2}=160^0\)
Mà AG là tia phân giác của \(\widehat{DAB}\left(gt\right)\)
Áp dụng tính chất tia phân giác nên: \(\widehat{BAG}=\frac{1}{2}\widehat{DAB}\)
Tượng tự ta có: \(\widehat{ABG}=\frac{1}{2}\widehat{ABC}\) ( Vì BG là tia phân giác góc ABC )
Tiếp tục xét tam giác ABG rồi dùng định lý tổng 3 góc trong 1 tam giác = 180 độ là ra
Bài này có trong sách giáo khoa nè
cho hình bình hành ABCD. Các tia pg của góc A,B,C,D cắt nhau tại các điểm E,F,G,H. cm rằng tứ giác EFGH là 1 hình chữ nhật
Cho hình bình hành ABCD. Các tia phân giác các góc A,B,C,D cắt nhau lần lượt tại E,F,G,H .Cm EFGH là hình chữ nhật
Cho hình bình hành ABCD, AB = 6cm, AD = 4cm. Các tia phân giác của các góc A, B, C, D cắt nhau tạo thành tứ giác EFGH.
a) Tứ giác EFGH là hình gì ?
b ) Tính độ dài đường chéo của tứ giác EFGH
c ) Hinh bình hành ABCD có thêm điều kiện gì để diện tích tứ giác EFGH lớn nhất ?
Cho hcn ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE/AB=AH/AD=CF/CB=CG/CD
a)cm/ tú giác EFGH là hbh
b)cm/ hbh EFGH có chu vi ko đổi
a) Xét tam giác ADB có:
\(\frac{AE}{AB}=\frac{AH}{AD}\left(gt\right)\)
\(\Rightarrow HE//DB\left(1\right)\)( định lý Ta-let đảo )
Xét tam giác CDB có:
\(\frac{CF}{CB}=\frac{CG}{CD}\left(gt\right)\)
\(\Rightarrow GF//BD\left(2\right)\)
Từ (1) và (2) \(\Rightarrow HE//GF\)
CMTT\(HG//EF\)( cùng // AC)
Xét tứ giác EFGH có:
\(\hept{\begin{cases}HE//GF\left(cmt\right)\\HG//EF\left(cmt\right)\end{cases}\Rightarrow EFGH}\)là hình bình hành (dhnb)
b)
Đặt\(\frac{AE}{AB}=\frac{AH}{AD}=\frac{CF}{CB}=\frac{CG}{CD}=k\)
Xét tam giác ADB có:
\(HE//BD\left(gt\right)\)
\(\Rightarrow\frac{HE}{BD}=\frac{AE}{AB}\)( hệ quả của định lý Ta-let)
\(\Rightarrow\frac{HE}{BD}=k\)( vì \(\frac{AE}{AB}=k\))
\(\Rightarrow HE=k.BD\)
Xét tam giác ABC có:
\(EF//AC\left(cmt\right)\)
\(\Rightarrow\frac{EF}{AC}=\frac{BE}{BA}\)( hệ quả của định lý Ta-let)
\(\Rightarrow\frac{EF}{AC}=\frac{AB-AE}{BA}=1-k\)
\(\Rightarrow EF=\left(1-k\right)AC\)
\(P_{EFGH}=2\left(HE+EF\right)\)
\(=2\left[k.BD+\left(1-k\right)AC\right]\)
\(=2AC\)không đổi ( AC=BD do ABCD là hình chữ nhật )
Vậy chu vi của hbh EFGH có giá trị không đổi