Question

cho hbh ABCD. các tia p/giác của các góc A, B, C, D cắt nhau như trên h.91. c/m EFGH là hcn

Answer 1

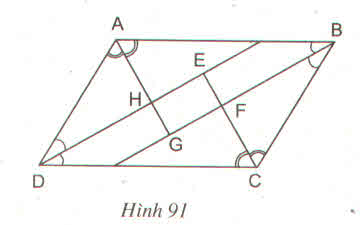
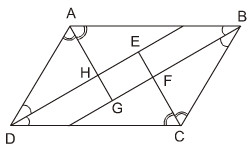
\(\widehat{HAD}+\widehat{HDA}=\dfrac{1}{2}\left(\widehat{BAD}+\widehat{ADC}\right)=\dfrac{1}{2}\cdot180^0=90^0\)

=>\(\widehat{AHD}=90^0\)

=>AG\(\perp\)DE

\(\widehat{GAB}+\widehat{GBA}=\dfrac{1}{2}\left(\widehat{BAD}+\widehat{ABC}\right)=\dfrac{1}{2}\cdot180^0=90^0\)

=>\(\widehat{AGB}=90^0\)

\(\widehat{FBC}+\widehat{FCB}=\dfrac{1}{2}\left(\widehat{ABC}+\widehat{BCD}\right)=\dfrac{1}{2}\cdot180^0=90^0\)

=>\(\widehat{BFC}=90^0\)

Xét tứ giác HEFG có \(\widehat{EHG}=\widehat{HGF}=\widehat{GFE}=90^0\)

nên HEFG là hình chữ nhật