Cho hình thang ABCD(AB//CD) gọi I là trung điểm của cạnh AC ,K là trung điểm của cạnh BD.CMR IK//CD
MM
Những câu hỏi liên quan
Cho hình thang ABCD (AB//CD). Gọi I,K,M lần lượt là trung điểm của AB, BD, AC và E là giao điểm của IK và CD. Chứng minh: IK=KE
Ta có: hình thang ABCD => AB//CD
=> Góc ABD = góc BDE ( cặp góc so le trong)
Xét tam giác IKB và tam giác EKD có:
Góc BKI = góc DKE ( đối đỉnh)
KB=KD ( K là trung điểm của BD)
Góc ABD = góc BDE ( cmt)
=> Tam giác IKB = tam giác EKD ( g-c-g)
=> IK=EK ( 2 cạnh tương ứng)
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB // CD), M là trung điểm của cạnh CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM và AC.
a) Chứng minh rằng IK // AB;
b) Đường thẳng IK cắt AD và BC theo thứ tự ở E và F. Chứng minh rằng EI = IK = KF.
Ban có đáp án câu này chưa cho mình xin với. Mình cũng đang học
Đúng 0
Bình luận (0)
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Đúng 0
Bình luận (0)
vân toàn sao vậy bài này thì sao đâu mà lại đăng nội quy
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thang cân ABCD (AB//CD). Gọi E là trung điểm của cạnh AB. Gọi I, K, M theo thứ tự là trung điểm của BC, CD, DA. EIKM là hình j??? vì saoo??
Xét ΔBAC có BE/BA=BI/BC
nên EI//AC và EI=AC/2
Xét ΔDAC có DK/DC=DM/DA
nên KM//AC và KM=AC/2
=>EI//KM và EI=KM
Xét ΔABD có AE/AB=AM/AD
nên EM//BD và EM=BD/2=AC/2=EI
Xét tứ giác EIKM có
EI//KM
EI=KM
EM=EI
Do đó: EIKM là hình thoi
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB // CD), M là trung điểm của cạnh CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM và AC.
a) Chứng minh rằng IK // AB;
b) Đường thẳng IK cắt AD và BC theo thứ tự ở E và F. Chứng minh rằng EI = IK = KF.
c)CD=a AB=b tính IK
ĐÂY LÀ TOÁN MÀ CÓ PHẢI NỘI DUNG KHÁC ĐÂU
Đúng 0
Bình luận (0)
ĐỪNG ẤN ĐỌC THÊM
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
Đã kêu đừng ấn mà đéo nghe :))))
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.Thôi, lướt tiếp đi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
Lần này nữa thôi :)))
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.Cố lên
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
Đúng 0
Bình luận (0)
a) Vì ABCD là hình thang nên ta có:
AB // CD (gt) (1)
⇒D1ˆ=B1ˆ⇒D1^=B1^ (2 góc so le trong) (2)
Và C1ˆ=A1ˆC1^=A1^ (2 góc so le trong) (3)
Xét ΔIMDΔIMD và ΔIABΔIAB ta có:
I1ˆ=I2ˆI1^=I2^ (2 góc đối đỉnh) (4)
Từ (2), (4) ⇒ΔIMD∼ΔIAB⇒ΔIMD∼ΔIAB (G-G) (5)
Xét ΔKMCΔKMC và ΔKBAΔKBA ta có:
K1ˆ=K2ˆK1^=K2^ (2 góc đối đỉnh) (6)
Từ (3), (6) ⇒ΔKMC∼ΔKBA⇒ΔKMC∼ΔKBA (G-G) (7)
Từ (5) ⇒IM / IA=DM / AB⇒IM / IA=DM / AB (8)
Từ (7) ⇒KM / KB=MC / AB⇒KM / KB=MC / AB (9)
Mà DM = MC (M là trung điểm của CD) (10)
⇒DM / AB=MC / AB⇒DM / AB=MC / AB (11)
Từ (8), (9), (11) ⇒IM / IA=KM / KB⇒IM / IA=KM / KB (12)
Nên IK // AB (định lý Ta-lét đảo) (13)
Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = l4cm. Tính độ dài MI, IK, KN.
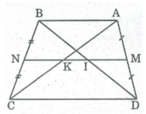
Hình thang ABCD có AB // CD
M là trung điểm của AD (gt)
N là trung điểm của BC (gt)
Nên MN là đường trung bình của hình thang ABCD ⇒ MN//AB// CD
MN = (AB + CD) / 2 = (6 + 14) / 2 = 10 (cm)
* Trong tam giác ADC, ta có:
M là trung điểm của AD
MK // CD
⇒ AK= KC và MK là đường trung bình của ∆ ADC.
⇒ MK = 1/2 CD = 1/2 .14= 7 (cm)
Vậy: KN = MN – MK = 10 – 7 = 3 (cm)
* Trong ∆ ADB, ta có:
M là trung điểm của AD
MI // AB nên DI = IB
⇒ MI là đường trung bình của ∆ DAB
⇒ MI = 1/2 AB = 1/2 .6 = 3 (cm)
IK = MK – Ml = 7 – 3 = 4 (cm)
Đúng 1
Bình luận (0)
Cho hình thang ABCD ( AB // CD; AB < CD). Gọi I là trung điểm của cạnh BD, K là trung điểm của cạnh AC. Từ I kẻ đường thẳng vuông góc với AD, từ K kẻ đường thẳng vuông góc với BC. Chúng cắt nhau tại O. Chứng minh: tam giác ODC cân
cho hình thang ABCD (AB// CD ) M là trung điểm của AD , N là trung điểm của BC. gỌI I, K THEO THỨ TỰ LẦN lượt là giao điểm của MN với BD,AC. cho biết AB = 6cm , CD = 14 cm . Tính độ dài ,MI,IK,KN
Cho hình thang ABCD (AB //CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = 14 cm. Tính độ dài MI, IK, KN ?
Cho hình thang ABCD (AB//CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I,K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB=6cm, CD = 14cm. Tính các độ dài MI,IK,KN.





