Question

Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = l4cm. Tính độ dài MI, IK, KN.

Answer 1

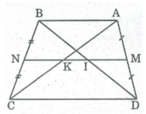
Hình thang ABCD có AB // CD

M là trung điểm của AD (gt)

N là trung điểm của BC (gt)

Nên MN là đường trung bình của hình thang ABCD ⇒ MN//AB// CD

MN = (AB + CD) / 2 = (6 + 14) / 2 = 10 (cm)

* Trong tam giác ADC, ta có:

M là trung điểm của AD

MK // CD

⇒ AK= KC và MK là đường trung bình của  ∆ ADC.

⇒ MK = 1/2 CD = 1/2 .14= 7 (cm)

Vậy: KN = MN – MK = 10 – 7 = 3 (cm)

* Trong  ∆ ADB, ta có:

M là trung điểm của AD

MI // AB nên DI = IB

⇒ MI là đường trung bình của ∆ DAB

⇒ MI = 1/2 AB = 1/2 .6 = 3 (cm)

IK = MK – Ml = 7 – 3 = 4 (cm)