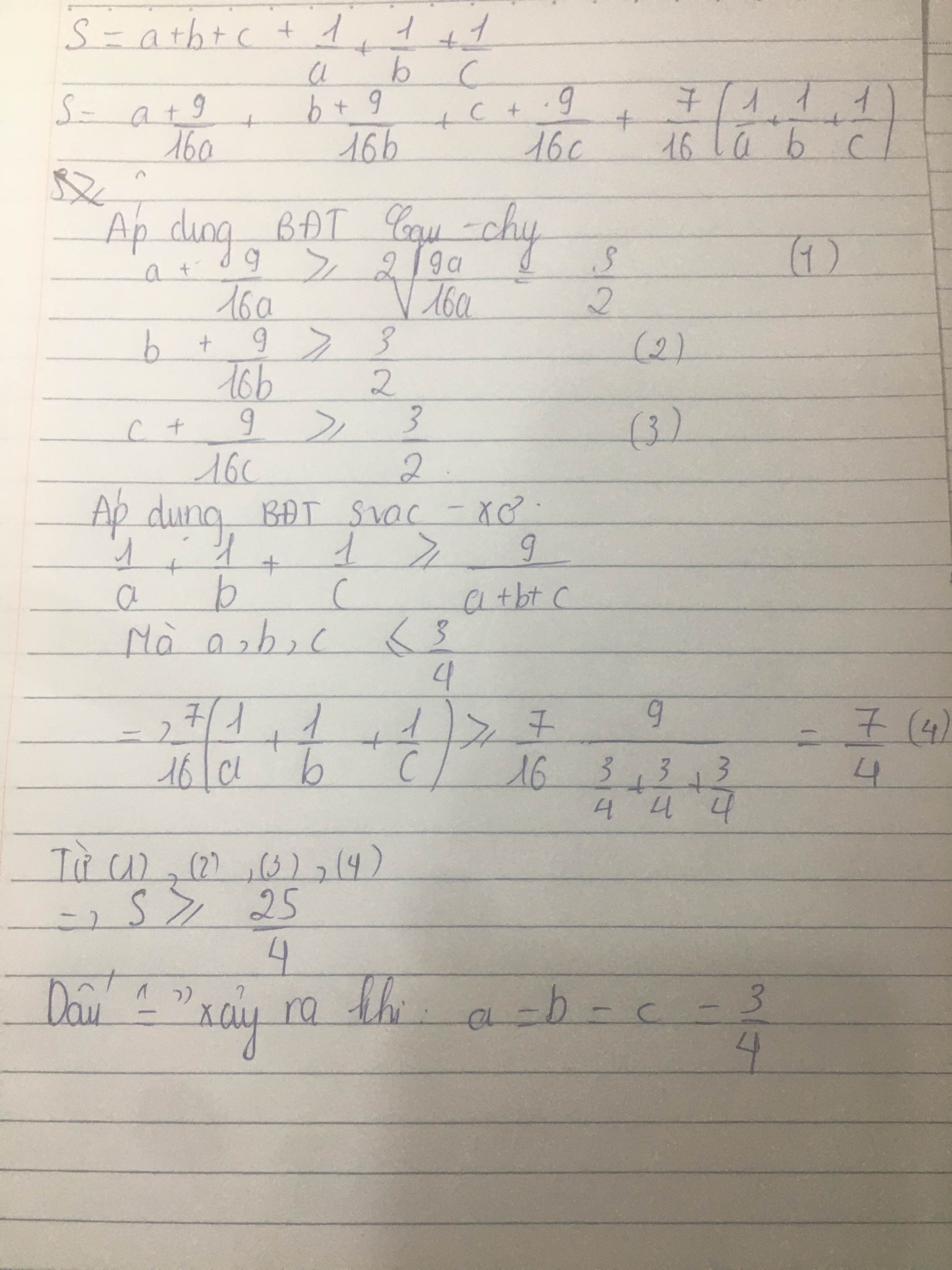Tìm giá trị nhỏ nhất của A=\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) với a,b,c > 0 và a+b+c=3abc.
VH
Những câu hỏi liên quan
Cho a,b,c>0 và \(a,b,c\le\dfrac{3}{4}\)
Tìm giá trị nhỏ nhất của S= \(a+b+c+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
giúp :)
Cho a,b,c>0 và a+b+c=3. Tìm giá trị nhỏ nhất của P=\(\dfrac{a}{1+b^2}+\dfrac{b}{1+c^2}+\dfrac{c}{1+a^2}\)
\(\dfrac{a}{1+b^2}=a-\dfrac{ab^2}{1+b^2}\ge a-\dfrac{ab^2}{2b}=a-\dfrac{1}{2}ab\)
Tương tự: \(\dfrac{b}{1+c^2}\ge b-\dfrac{1}{2}bc\) ; \(\dfrac{c}{1+a^2}\ge c-\dfrac{1}{2}ca\)
Cộng vế:
\(P\ge a+b+c-\dfrac{1}{2}\left(ab+bc+ca\right)\ge a+b+c-\dfrac{1}{6}\left(a+b+c\right)^2=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(a=b=c=1\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức:
a,A=\(\dfrac{x+1}{\sqrt{x}-2}\) với x>4
b,B=\(\dfrac{bc}{a^2b+a^2c}+\dfrac{ac}{b^2a+b^2c}+\dfrac{ab}{c^2a+c^2b}\) với a,b,c>0 và abc=1
\(A=\dfrac{x-4+5}{\sqrt{x}-2}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)+5}{\sqrt{x}-2}=\sqrt{x}+2+\dfrac{5}{\sqrt{x}-2}\)
\(=\sqrt{x}-2+\dfrac{5}{\sqrt{x}-2}+4\ge2\sqrt{\dfrac{5\left(\sqrt{x}-2\right)}{\sqrt{x}-2}}+4=4+2\sqrt{5}\)
\(A_{min}=4+2\sqrt{5}\) khi \(9+4\sqrt{5}\)
b.
Đặt \(\left(a;b;c\right)=\left(\dfrac{1}{x};\dfrac{1}{y};\dfrac{l}{z}\right)\Rightarrow xyz=1\)
\(B=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\ge\dfrac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(B_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\Rightarrow a=b=c=1\)
Đúng 0
Bình luận (2)
cho a,b,c > 0 tìm giá trị nhỏ nhất của 2( a + b + c ) + \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) Khi a2+b2+c2 = 3
Cho a,b,c>0 và a+b+c=1.
Tìm giá trị nhỏ nhất của: A= \(\dfrac{1}{1-2\left(ab+ac+bc\right)}\)+\(\dfrac{1}{abc}\)
SỬ DỤNG BẤT ĐẲNG THỨC BUNHIACOPXKI
Cho a,b,c>0 thỏa mãn a+b+c=1. Tìm giá trị nhỏ nhất của biểu thức
P=\(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}+\dfrac{1}{a^2+b^2+c^2}\)
MN giúp e với
\(P=\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ac}+\dfrac{1}{a^2+b^2+c^2}\ge\dfrac{\left(1+1+1\right)^2}{ab+bc+ca}+\dfrac{1}{a^2+b^2+c^2}\) (BĐT Cauchy Schwarz)
\(=\dfrac{9}{ab+bc+ca}+\dfrac{1}{a^2+b^2+c^2}\)
\(=\dfrac{1}{ab+bc+ca}+\dfrac{1}{ab+bc+ca}+\dfrac{1}{a^2+b^2+c^2}+\dfrac{7}{ab+bc+ca}\)
\(\ge\dfrac{\left(1+1+1\right)^2}{a^2+b^2+c^2+2ab+2ac+2bc}+\dfrac{7}{ab+bc+ca}\)
\(=\dfrac{9}{\left(a+b+c\right)^2}+\dfrac{7}{ab+bc+ca}\)
Ta có: \(ab+bc+ca\le\dfrac{\left(a+b+c\right)^2}{3}=\dfrac{1}{3}\) .Thế vào biểu thức
\(\Rightarrow P\ge9+\dfrac{7}{\dfrac{1}{3}}=9+21=30\)
\(\Rightarrow P_{min}=30\) khi \(a=b=c=\dfrac{1}{3}\)
Đúng 2
Bình luận (1)
a) Tìm giá trị nhỏ nhất của biểu thức \(x^2-8x+5\)
b) Cho \(a^3+b^3+c^3=3abc\) và \(a+b+c\) ≠ 0
Tính giá trị của biểu thức N =\(\dfrac{a^2+b^2+c^2}{\left(a+b+c\right)^2}\)
Cho a,b,c >0 và \(a+b+c=1\). Tính giá trị nhỏ nhất của biểu thức:
\(P=\dfrac{a}{4-3a}+\dfrac{b}{4-3b}+\dfrac{c}{4-3c}\)
\(P=\dfrac{a}{4-3a}+\dfrac{b}{4-3b}+\dfrac{c}{4-3c}=\dfrac{a^2}{4a-3a^2}+\dfrac{b^2}{4b-3b^2}+\dfrac{c^2}{4c-3c^2}\)
\(\ge\dfrac{\left(a+b+c\right)^2}{4\left(a+b+c\right)-3\left(a^2+b^2+c^2\right)}\) (BĐT Cauchy-Schwarz)
\(=\dfrac{1}{4-3\left(a^2+b^2+c^2\right)}\)
Ta có: \(3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\)
\(\Rightarrow4-3\left(a^2+b^2+c^2\right)\le4-\left(a+b+c\right)^2=4-1=3\)
\(\Rightarrow\dfrac{1}{4-3\left(a^2+b^2+c^2\right)}\ge\dfrac{1}{3}\)
\(\Rightarrow P_{min}=\dfrac{1}{3}\) khi \(a=b=c=\dfrac{1}{3}\)
Đúng 4
Bình luận (0)
Casch2:đặt \(\left\{{}\begin{matrix}4-3a=x\\4-3b=y\\4-3c=z\end{matrix}\right.\)\(=>\left\{{}\begin{matrix}a=\dfrac{4-x}{3}\\b=\dfrac{4-y}{3}\\c=\dfrac{4-z}{3}\end{matrix}\right.\)\(x+y+z=9\)
\(=>P=\dfrac{4-x}{3x}+\dfrac{4-y}{3y}+\dfrac{4-z}{3z}=\dfrac{4}{3x}+\dfrac{4}{3y}+\dfrac{4}{3z}-\left(\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}\right)\)
\(=\dfrac{\left(2+2+2\right)^2}{3.9}-1=\dfrac{4}{3}-1=\dfrac{1}{3}\)
dấu"=" xảy ra<=>x=y=z=3<=>a=b=c=1/3
Đúng 4
Bình luận (0)
a)Tìm giá trị nhỏ nhất của biểu thức Q=\(\dfrac{x^2-4x+1}{x^2}\)
b)Tìm a,b,c∈N*:(a-\(\dfrac{1}{b}\))(b-\(\dfrac{1}{c}\))(c-\(\dfrac{1}{a}\))∈N*
HELP