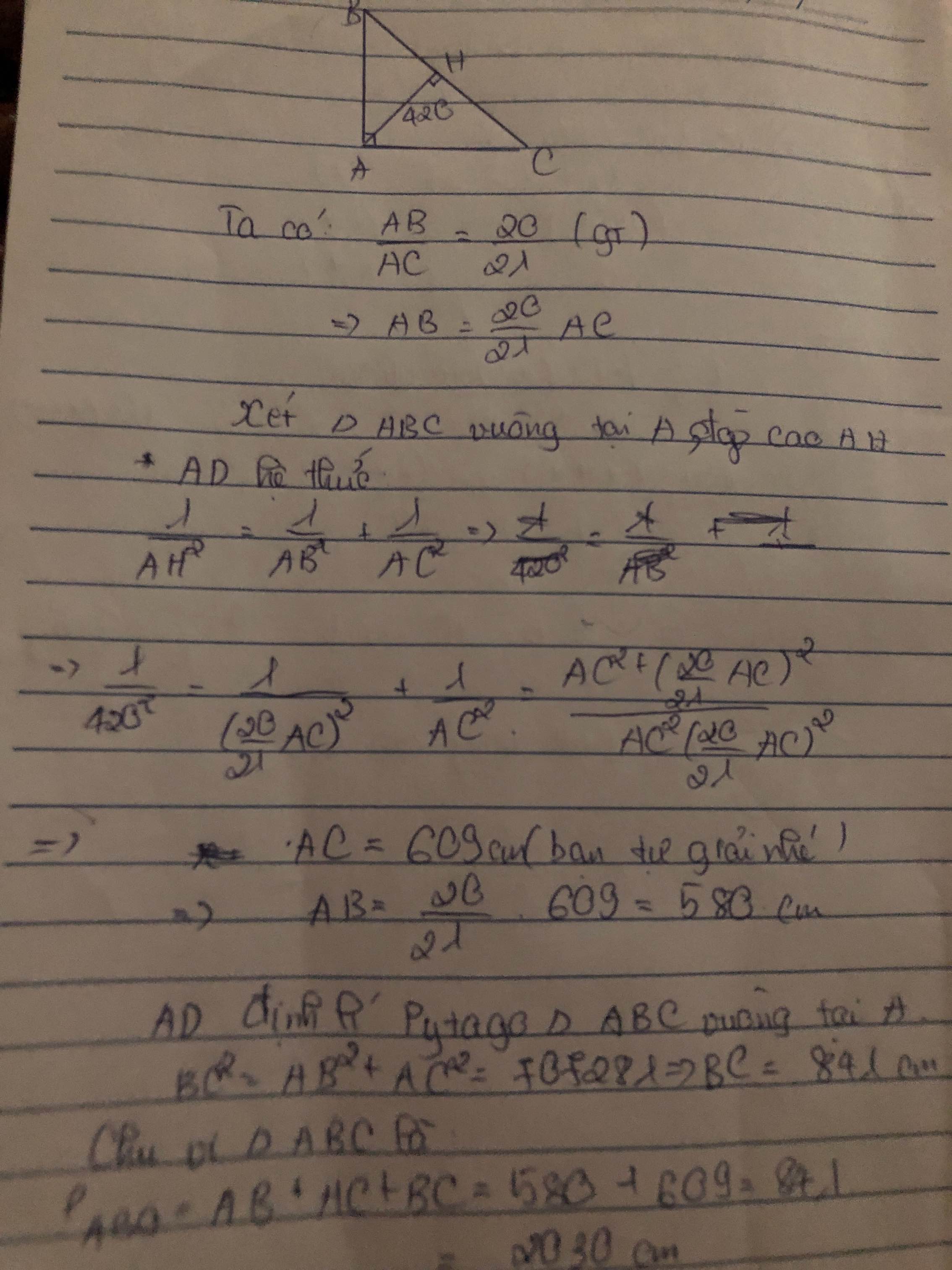Cho tam giác ABC vuông tại A, đường cao AH. Tính chu vi tam ABC, biết rằng: CH=20 cm. Góc B=60°
NL
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. Tính chu vi tam giác ABC, biết rằng CH = 20,3 cm và góc B bằng 620 . (Chính xác dến 6 chữ số thập phân)
Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{C}=28^0\)
Xét ΔACH vuông tại H có
\(AH=CH\cdot\tan28^0\)
\(=20.3\cdot\tan28^0\)
\(\Leftrightarrow AH\simeq10,793701\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AH^2+CH^2=AC^2\)
\(\Leftrightarrow AC^2=10.793701^2+20.3^2\)
hay \(AC\simeq22,991172\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB\simeq5,739112\left(cm\right)\)
\(\Leftrightarrow BC\simeq26.093112\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AB\simeq12,339226\left(cm\right)\)
Chu vi tam giác ABC là:
C=AB+AC+BC
\(=12.339226+22.991172+26.093112\)
\(=64.423510\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn. Kẻ AH vuông góc với BC tại H. Biết rằng AC = 20 cm, AH = 12 cm, BH = 5 cm. Tính chu vi của tam giác ABC.
AB = 13 cm, BC = 21 cm.
Từ đó, chu vi của tam giác ABC là 54 cm.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 15 cm, HC = 9 cm. Tính chu vi tam giác ABH và góc B là tròn đến độ.
\(BC=\dfrac{15^2}{9}=25\left(cm\right)\)
BH=25-9=16cm
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
AB=căn(16^2+12^2)=20cm
C=16+12+20=28+20=48cm
Xét ΔABC vuông tại A có sin B=AC/BC=3/5
nên góc B=37 độ
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, vẽ đường cao AH, biết chu vi tam giác AHB = 30 cm, chu vi tam giác CHA = 40 cm. Tính chu vi tam giác ABC
cách 1
Đề bài có đủ điều kiện để tính. Sau khi xác định được tỷ lệ các cạnh tg ABC là a:b:c=5:4:3, đặt AB=3t, AC=4t; BC=5t (như bạn Hải đã chứng minh). Vì tam giác ABC vuông ta có AB^2=BH.BC ---> (3t)^2=BH.(5t) ---> BH=1,8.t
----> AH^2=AB^2-BH^2 =(3t)^2 -(1,8t)^2 = 9t^2 -3,24t^2 =5,76t^2 --> AH= 2,4t
Chu vi ABH=30 --> AB+BH+AH=30 --> 3t+1,8t+2,4t=30 --->7,2t=30 ---> t= 25/6
Chu vi ABC= 3t+4t+5t= 12t =12.(25/6) =50 cm
cách 2
Tam giác ABH và CAH vuông và có ^BAH=^C (cùng phụ với góc B)
Nên Tam giác ABH và CAH đồng dạng (g-g) =>AB/AC = k (tỷ số đồng dạng)
Mà C(ABH) / C(CAH) = k (tỷ số chu vi bằng tỷ số đồng dạng)
suy ra 30/40 = k hay k = 3/4.
do đó AB/AC = 3/4 hay AB/3 = AC/4 = t
=> AB = 3t; AC = 4t Theo Pitago ta tính được BC = 5t.
Vậy chu vi tam giác ABC là AB+AC+BC = 3t+4t+5t = 12t.
k mk nha!!^-^
Đúng 1
Bình luận (0)
Sau khi xác định được tỷ lệ các cạnh tg ABC là a:b:c=5:4:3, đặt AB=3t, AC=4t; BC=5t . Vì tam giác ABC vuông ta có AB^2=BH.BC => (3t)^2=BH.(5t) => BH=1,8.t
=> AH^2=AB^2-BH^2 =(3t)^2 -(1,8t)^2 = 9t^2 -3,24t^2 =5,76t^2 --> AH= 2,4t
Chu vi ABH=30 --> AB+BH+AH=30 --> 3t+1,8t+2,4t=30 --->7,2t=30 ---> t= 25/6
Chu vi ABC= 3t+4t+5t= 12t =12.(25/6) =50 cm
Đáp số : 50 cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, biết góc B=44 độ, AH=9cm, tính chu vi tam giác ABC
cho tam giác ABC vuông tại A đường cao AH ; biết chu vi của tam giác ABC là 50 cm ; chu vi của tam giác ABH là 30 cm : chu vi của tam giác ACH bằng 40 cm tính AH
Theo bài ra ta có
AB + AH + BH = 30
AC + CH + AH = 40
AB + BC + AC = 50
Khi đó AB + AH + BH + AC + CH + AH = 70
=> AB + AC + (BH + CH) + 2AH = 70
=> AB + AC + BC + 2AH = 70
=> 50 + 2AH = 70
=> AH = 10
Vậy AH = 10 cm
Cho tam giác vuông ABC, đường cao AH, cạnh góc vuông AC = 60 cm, cạnh huyền BC = 100 cm. Tính chu vi tam giác ABC, ABH, ACH
Hình vẽ chỉ mang tính chất minh họa
Áp dụng định lý Py-ta-go vào tam giác vuông ABC:
\(AB=\sqrt{BC^2-AC^2}\)
\(\Rightarrow AB=\sqrt{100^2-60^2}\)
\(\Rightarrow AB=80\left(cm\right)\)
Chu vi tam giác ABC= AB+AC+BC=80+60+100=240(cm)
Xét tam giác ABC vuông tại A, đương cao AH có:
+ \(AH=\frac{AB.AC}{BC}\)
\(\Rightarrow AH=\frac{80.60}{100}\)
\(\Rightarrow AH=48\left(cm\right)\)
+ \(BH=\frac{AB^2}{BC}\)
\(\Rightarrow BH=\frac{80^2}{100}=64\left(cm\right)\)
\(CH=BC-BH\)
\(\Rightarrow CH=100-64=36\left(cm\right)\)
Chu vi tam giác ABH= AB+BH+AH=80+64+48=192(cm)
Chu vi tam giác ACH=AC+CH+AH=60+36+48=144(cm)
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết chu vi tam giác AHB là 30 cm, chu vi tam giác AHC là 40 cm. Tính chu vi tam giác ABC.
Ta có hình vẽ
Ta có : ΔABH + ΔACH = ΔABC
Hay: 30 + 40 = ΔABC
=> ΔABC = 70 cm
mk k bít dug hay sai đâu đó...
mk chỉ thử lm thui ak^^^
Đúng 0
Bình luận (2)
Cho tam giác ABC vuông tại A , đường cao AH . Biết AB/AC = 20/21 , AH = 420 . Tính chu vi tam giác ABC
\(\dfrac{AB}{AC}=\dfrac{20}{21}\Rightarrow AB=\dfrac{20AC}{21}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{841}{400AC^2}\)
\(\Rightarrow AC=609\) \(\Rightarrow AB=\dfrac{20}{21}AC=580\)
\(BC=\sqrt{AB^2+AC^2}=841\)
Chu vị: \(609+580+841=2030\)
Đúng 2
Bình luận (0)
Ta có: \(\dfrac{AB}{AC}=\dfrac{20}{21}\)
nên \(AB=\dfrac{20}{21}\cdot AC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{\dfrac{400}{441}AC^2}+\dfrac{\dfrac{400}{441}}{\dfrac{400}{441}AC^2}=\dfrac{1}{176400}\)
\(\Leftrightarrow\dfrac{400}{441}AC^2=336400\)
\(\Leftrightarrow AC^2=370881\)
hay AC=609(cm)
\(\Leftrightarrow AB=\dfrac{20}{21}\cdot AC=\dfrac{20}{21}\cdot609=580\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=580^2+609^2=371461\)
hay BC=841(cm)
Chu vi tam giác ABC là:
AB+AC+BC=580+609+841=2030(cm)
Đúng 2
Bình luận (0)