 giúp mình đưa về dạng ax+by=c với ạ
giúp mình đưa về dạng ax+by=c với ạ
TT
Những câu hỏi liên quan
Minh có đang học toán nâng cao ở dạng tìm min max , nhưng có bài muốn tìm min max phải đưa về dạng ( a +b +c )2 nhưng mà khó quá , ai có mẹo nào giúp đưa biết thức đó về dạng ( a +b +c ) 2 không ạ giúp mình với
dồn a , dồn b là xong
( c là hằng số )
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho nửa đường tròn tâm O , đường kính AB. Kẻ 2 tiếp tuyến Ax , By cùng phía với nửa đường tròn đối với AB. Gọi C là 1 điểm trên tia Ax kẻ tiếp tuyến CM với nửa đường tròn( M là tiếp điểm ), CM cắt By ở D. ( Vẽ hình giúp mình với ạ)a. Tính số đo góc CODb. Gọi i là giao điểm của OC và AM, K là giao điểm của OD và MB. Tứ giác OIMK là hình gì? Vì sao?c. C/m tích AC.BD không đổi khi C di chuyển trên Axd. C/m AB là tiếp tuyến của đường tròn đường kính CD.giúp mình giải với ạ, mình cảm ơn
Đọc tiếp
Cho nửa đường tròn tâm O , đường kính AB. Kẻ 2 tiếp tuyến Ax , By cùng phía với nửa đường tròn đối với AB. Gọi C là 1 điểm trên tia Ax kẻ tiếp tuyến CM với nửa đường tròn( M là tiếp điểm ), CM cắt By ở D. ( Vẽ hình giúp mình với ạ)
a. Tính số đo góc COD
b. Gọi i là giao điểm của OC và AM, K là giao điểm của OD và MB. Tứ giác OIMK là hình gì? Vì sao?
c. C/m tích AC.BD không đổi khi C di chuyển trên Ax
d. C/m AB là tiếp tuyến của đường tròn đường kính CD.
giúp mình giải với ạ, mình cảm ơn
đưa ra dạng đúng của từ:
I am ...... sick today. I can't go to school ( real )
mn giúp mình với ạ
| Viết dười dạng tích các tổng sau: 1/ ab + ac 2/ ab – ac + ad 3/ ax – bx – cx + dx 4/ a(b + c) – d(b + c) 5/ ac – ad + bc – bd 6/ ax + by + bx + ay |
giúp mình với mình đang cần gấp
1/ ab+ac=a.b+a.c=a(b+c)
Đưa về dạng tích rồi tính:
A=652+60.65+152-202 GIÚP MÌNH VỚI
\(A=65^2+60\cdot65+15^2-20^2\)
\(=65^2+2\cdot65\cdot30+30^2-1075\)
\(=95^2-1075\)
=7950
Đúng 1
Bình luận (0)
Đưa về dạng tích : A=ab(a-b)(c+1)+bc(b-c)(a+1)+ca(c-a)(b+1)
bạn nào giải đc giúp mình với mình cần gấp
Giải các hệ phương trình theo hai cách:*Cách thứ nhất: đưa hệ phương trình về dạng:
a
x
+
b
y
c
a
x
+
b...
Đọc tiếp
Giải các hệ phương trình theo hai cách:
*Cách thứ nhất: đưa hệ phương trình về dạng: a x + b y = c a ' x + b ' y = c '
*Cách thứ hai: đặt ẩn phụ, chẳng hạn s = 3x – 2, t = 3y + 2
2 3 x - 2 - 4 = 5 3 y + 2 4 3 x - 2 + 7 3 y + 2 = - 2
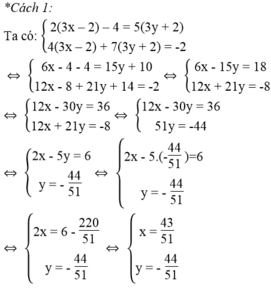
Vậy hệ phương trình đã cho có nghiệm (x; y) = (43/51 ; -44/51 )
*Cách 2: Đặt m = 3x – 2, n = 3y + 2
Ta có hệ phương trình:
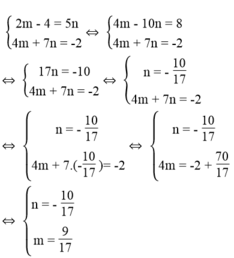
Ta có: 3x – 2 = 9/17 ⇔ 3x = 2 + 9/17 ⇔ 3x = 43/17 ⇔ x = 43/51
3y + 2 = - 10/17 ⇔ 3y = -2 - 10/17 ⇔ 3y = - 44/17 ⇔ y = - 44/51
Vậy hệ phương trình đã cho có nghiệm (x; y) = (43/51 ; -44/51 )
Đúng 0
Bình luận (0)
1/x+1=0 có phải phương trình bậc nhất 1 ẩn không ? (đưa về dạng ax+b=0 giúp mình)
Đặt thừa số chung, viết tổng thành tích
a) ab - 2b - 3a + 6
b) ax - by - ay + bx
c) ax + by - ay - bx
d) a^2 - (b + c) a + bc
e) (3a - 2)(4a - 3) -(2 - 3a)(3a + 1)
f) ax + ay + az - bx - by - bz - x -y -z
Các bạn ơi giúp mình với! mÌnh ko hiểu gì lun! Bạn nào giải đc câu nào thì hay câu đó! cảm ơn nhìu ạ!
a/ \(ab-2b-3a+6=\left(ab-2b\right)-\left(3a-6\right)=b\left(a-2\right)-3\left(a-2\right)=\left(a-2\right)\left(b-3\right)\)
b/ \(ax-by-ay+bx==\left(ax+bx\right)-\left(by+ay\right)=x\left(a+b\right)-y\left(b+a\right)=\left(a+b\right)\left(x-y\right)\)
c/ \(ax+by-ay-bx=\left(ax-ay\right)+\left(by-bx\right)=a\left(x-y\right)+b\left(y-x\right)=a\left(x-y\right)-b\left(x-y\right)=\left(x-y\right)\left(a-b\right)\)
d/ \(a^2-\left(b+c\right)a+bc=a^2-ab-ac+bc=\left(a^2-ac\right)+\left(ab-bc\right)=a\left(a-c\right)+b\left(a-c\right)=\left(a-c\right)\left(a+b\right)\)e/ \(\left(3a-2\right)\left(4a-3\right)-\left(2-3a\right)\left(3a+1\right)=\left(3a-2\right)\left(4a-3\right)+\left(3a-2\right)\left(3a+1\right)=\left(3a-2\right)\left(4a-3+3a+1\right)=\left(3a-2\right)\left(7a-2\right)\)
f/ \(ax+ay+az-bx-by-bz-x-y-z=\left(ax+ay+az\right)-\left(bx+by+bz\right)-\left(x+y+z\right)\)
\(=a\left(x+y+z\right)-b\left(x+y+z\right)-\left(x+y+z\right)=\left(x+y+z\right)\left(a-b-1\right)\)
Đúng 0
Bình luận (0)



