\(x=3y\); \(y-x=26\)

từ \(y-x=26\Rightarrow x=y-26\)

thay \(x=y-26\), ta được:

\(y-26=3y\)

\(\Rightarrow2y=-26\)

\(\Rightarrow y=-13\)mà  \(x=3y\Rightarrow x=3\cdot\left(-13\right)=-39\)

vậy \(x=-39;y=-13\)

Ta có : \(\frac{x}{5}=\frac{y}{7}\Rightarrow5y=7x\Rightarrow x=\frac{5y}{7}\)

Thay \(x=\frac{5y}{7}\)vào biểu thức \(2x+y=26\);ta được: 

\(\frac{2.5y}{7}+y=26\Rightarrow10y+7y=26.7\Rightarrow17y=182\Rightarrow y=\frac{182}{17}\)

Do đó : \(x=\frac{\frac{5.182}{17}}{7}=\frac{130}{17}\)

\(2x=3y=4z\\ =>\dfrac{2x}{12}=\dfrac{3y}{12}=\dfrac{4z}{12}\\ =>\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{x+y+z}{6+4+3}=\dfrac{26}{13}=2\\ =>x=2.6=12,y=2.4=8,z=2.3=6\)

1 CUA HANG SAU BUOI SANG BAN DI 88,5 KG GAO VAO BUI CHIEU BAN DI 76 KG THI CON LAI 72,55 KG GAO .HOI LUC DAU CUA HANG CO TAT CA BAO NHIEU KG GAO

+, \(\hept{\begin{cases}x-2=1\\2y+3=26\end{cases}\Rightarrow}\hept{\begin{cases}x=3\\y=\frac{23}{2}\end{cases}}\) loại

+, \(\hept{\begin{cases}x-2=26\\2y+3=1\end{cases}\Rightarrow\hept{\begin{cases}x=28\\y=-1\end{cases}}}\)loại

+, \(\hept{\begin{cases}x-2=2\\2y+3=13\end{cases}\Rightarrow\hept{\begin{cases}x=4\\y=5\end{cases}}}\)nhận

+, \(\hept{\begin{cases}x-2=13\\2y+3=2\end{cases}\Rightarrow\hept{\begin{cases}x=15\\y=-\frac{1}{2}\end{cases}}}\)loại

\(\Rightarrow x=4;y=5\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\frac{x}{2}=\frac{y}{3}=\frac{2x}{2.2}=\frac{3y}{3.3}=\frac{2x+3y}{4+9}=\frac{26}{13}=2\)

\(\frac{x}{2}=2\Rightarrow x=2.2=4\)

\(\frac{y}{3}=2\Rightarrow y=2.3=6\)

Vậy x=4 và y=6

\(\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{2x}{4}=\frac{3y}{9}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\frac{2x}{4}=\frac{3y}{9}=\frac{2x+3y}{4+9}=\frac{26}{13}=2\)

\(\frac{x}{2}=2\Rightarrow x=4;\frac{y}{3}=2\Rightarrow y=6\)

Từ 2x=3y=4z

=>\(\frac{2x}{12}=\frac{3y}{12}=\frac{4z}{12}\)

=>\(\frac{x}{6}=\frac{y}{4}=\frac{z}{3}\)

Theo TCDTSBN:

\(\frac{x}{6}=\frac{y}{4}=\frac{z}{3}=\frac{x+y+z}{6+4+3}=\frac{26}{13}=2\)

Vì x/6=2=>x=12

y/4=2=>y=8

z/3=2=>z=6

Vậy.......................

giải thích thêm:

Vì BCNN(2;3;4)=12 nên 2x/12=.....

Thanks nha Hoàng Phúc !

\((x-6)(3x-9)>0\)
TH1:
\(\orbr{\begin{cases}x-6< 0\\3x-9< 0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x< 6\\x< 3\end{cases}}\)\(\Rightarrow x< 3\)
TH2:
\(\orbr{\begin{cases}x-6>0\\3x-9>0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x>6\\x>3\end{cases}}\)\(\Rightarrow x>6\)
Vậy \(x< 3\) hoặc \(x>6\)thì \((x-6)(3x-9)>0\)
Học tốt!

20.
\((2x-1)(6-x)>0\)
TH1:
\(\orbr{\begin{cases}2x-1>0\\6-x>0\end{cases}\Rightarrow\orbr{\begin{cases}x< \frac{1}{2}\\x< 6\end{cases}}\Rightarrow x< 6}\)
TH2
\(\orbr{\begin{cases}2x-1< 0\\6-x< 0\end{cases}\Rightarrow\orbr{\begin{cases}x>\frac{1}{2}\\x>6\end{cases}}\Rightarrow x>\frac{1}{2}}\)
Vậy \(x< 6\)hoặc \(x>\frac{1}{2}\)thì \((2x-1)(6-x)>0\)
 

21.
\((2-x)(x+7)< 0\)
TH1.
\(\orbr{\begin{cases}2-x>0\\x+7< 0\end{cases}\Rightarrow\orbr{\begin{cases}x< 2\\x>-7\end{cases}}\Rightarrow-7< x< 2}\)
TH2.
\(\orbr{\begin{cases}2-x< 0\\x+7>0\end{cases}\Rightarrow\orbr{\begin{cases}x>2\\x< -7\end{cases}}\Rightarrow2< x< -7}\)(vô lí)
Vậy \(-7< x< 2\) thì \((2-x)(x+7)< 0\)
 

1) \(\left(x+1\right)^2=x^2+2x+1\)

2) \(\left(2x+1\right)^2=4x^2+4x+1\)

3) \(\left(2x+y\right)^2=4x^2+4xy+y^2\)

4) \(\left(2x+3\right)^2=4x^2+12x+9\)

5) \(\left(3x+2y\right)^2=9x^2+12xy+4y^2\)

6) \(\left(2x^2+1\right)^2=4x^4+4x^2+1\)

7) \(\left(x^3+1\right)^2=x^6+2x^3+1\)

8) \(\left(x^2+y^3\right)^2=x^4+2x^2y^3+y^6\)

9) \(\left(x^2+2y^2\right)^2=x^4+4x^2y^2+4y^4\)

10) \(\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^2=\dfrac{1}{4}x^2+\dfrac{1}{3}xy+\dfrac{1}{9}y^2\)

x 2 + 3 y = 5 4 x y + 6 2 y = 5 4 4 x y + 6 = 10 y 2 x y + 12 = 5 y 2 x y − 5 y = − 12 y 2 x − 5 = − 12

Vì x,y nguyên; 2x-5  − 12 = 1. − 12 = 12. − 1 = 2. − 6 = 6. − 2 = 3. − 4 = 4. − 3

nên

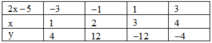
Vậy  x ; y = − 1 ; 4 ;    2 ; 12 ;    3 ; − 12 ;    4 ; − 4

\(a,VP=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\\ =\left(x+2y\right)\left[x^2-x.2y+\left(2y\right)^2\right]\\ =x^3+\left(2y\right)^3=x^3+8y^3=VT\left(đpcm\right)\\ b,VT=\left(x-y\right)\left(x^2+xy+y^2\right)-3xy\left(x-y\right)\\ =x^3-y^3-3xy\left(x-y\right)\\ =x^3-3x^2y+3xy^2-y^3\\ =\left(x-y\right)^3=VP\left(đpcm\right)\)

\(c,VT=\left(x-3y\right)\left(x^2+3xy+9y^2\right)-\left(3y+x\right)\left(9y^2-3xy+x^2\right)\\ =\left(x-3y\right)\left[x^2+x.3y+\left(3y\right)^2\right]-\left(x+3y\right).\left[x^2-x.3y+\left(3y\right)^2\right]\\ =x^3-27y^3-\left(x^3+27y^3\right)\\ =-54y^3=VP\left(đpcm\right)\)