Chứng minh: Hàm số y=f(x) =ax3(a khác 0) ĐB trên R khi a>0 và NB trên R khi a<0
Cho hàm số y = f x = ax 3 + bx 2 + cx + d , a ≠ 0 là hàm số lẻ trên R. Khi đó khẳng định nào sau đây là đúng?
A. a = c = 0
B. d = 0 , b ≠ 0
C. b = 0 , d ≠ 0
D. b = d = 0
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 2x}}{x}}&{khi\,\,x \ne 0}\\a&{khi\,\,x = 0}\end{array}} \right.\).
Tìm \(a\) để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\), \(f\left( x \right) = \frac{{{x^2} - 2x}}{x}\) là hàm phân thức hữu tỉ nên liên tục trên từng khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Ta có: \(f\left( 0 \right) = a\)
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \frac{{{x^2} - 2x}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{x\left( {x - 2} \right)}}{x} = \mathop {\lim }\limits_{x \to 0} \left( {x - 2} \right) = 0 - 2 = - 2\)
Để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thì hàm số \(y = f\left( x \right)\) phải liên tục tại điểm \({x_0} = 0\). Khi đó:
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow a = - 2\).
Vậy với \(a = - 2\) thì hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d với a , b , c ∈ R ; a > 0 và d > 2018 a + b + c + d - 1018 < 0 .
Số cực trị của hàm số y=|f(x)-1018| bằng
A. 3
B. 2
C. 1
D. 5
Đáp án D
Ta có hàm số g x = f x - 2018 là hàm số bậc ba liên tục trên R.
Do a>0 nên l i m x → - ∞ g ( x ) = - ∞ ; l i m x → + ∞ g ( x ) = + ∞
Để ý g 0 = d - 2018 > 0 ; g 1 = a + b + c + d - 2018 < 0 nên phương trình g(x)=0 có đúng 3 nghiệm phân biệt trên R.
Khi đó đồ thị hàm số g x = f x - 2018 cắt trục hoành tại 3điểm phân biệt nên hàm số y = f x - 2018 có đúng 5 cực trị.
Hàm số y = a x 3 + b x 2 + c x + d , a ≠ 0 luôn đồng biến trên ℝ khi và chỉ khi
A. a > 0 b 2 − a c < 0
B. a > 0 b 2 − 3 a c < 0
C. a > 0 b 2 − 3 a c > 0
D. a > 0 b 2 − 3 a c ≤ 0
Đáp án D
Ta có: Hàm số luôn đồng biến trên
ℝ ⇔ y ' = 3 a x 2 + 2 b x + c ≥ 0 ∀ x ∈ ℝ ⇔ a > 0 Δ y ' = b 2 − 3 a c ≤ 0
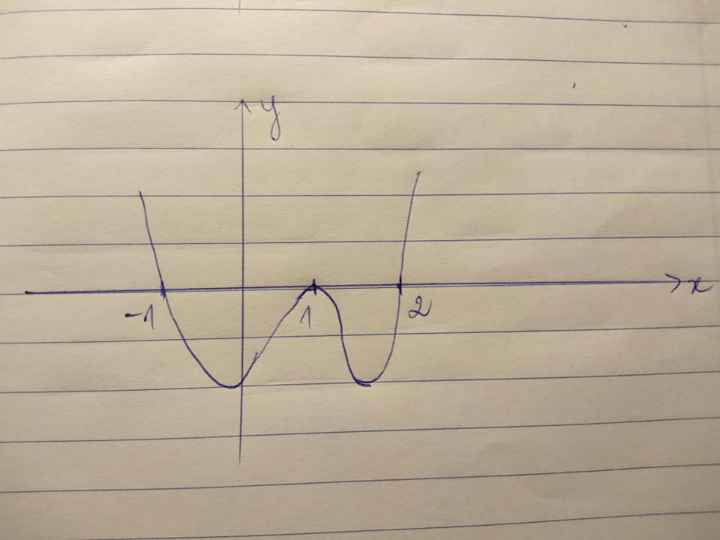
Cho hàm số y=f(x) liên tục trên R có đồ thị y=f '(x) như hình vẽ:
a)Tìm min, max của hàm số g(x)=f(\(\sqrt{8-x^2-2x}-1\))
b)Xác định khoảng đb, nb, cực đại, cực tiểu của g(x)=f(x2+x)
a.
TXĐ: \(D=\left[-4;2\right]\)
\(0\le\sqrt{9-\left(x+1\right)^2}\le3\Rightarrow-1\le\sqrt{9-\left(x+1\right)^2}\le2\)
\(\Rightarrow f'\left(\sqrt{8-x^2-2x}-1\right)\le0\) ; \(\forall x\in D\)
\(g'\left(x\right)=-\dfrac{x+1}{\sqrt{8-x^2-2x}}.f'\left(\sqrt{8-x^2-2x}-1\right)\) luôn cùng dấu \(x+1\)
\(\Rightarrow g\left(x\right)\) đồng biến trên \(\left[-1;2\right]\) và nghịch biến trên \(\left[-4;-1\right]\)
Từ BBT ta thấy \(g\left(x\right)_{max}=g\left(-4\right)=g\left(2\right)=f\left(-1\right)=?\)
\(g\left(x\right)_{min}=g\left(-1\right)=f\left(2\right)=?\)
(Do đề chỉ có thế này nên ko thể xác định cụ thể được min-max)
b.
\(g'\left(x\right)=\left(2x+1\right).f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\f'\left(x^2+x\right)=0\left(1\right)\end{matrix}\right.\)
Xét (1), ta chỉ cần quan tâm 2 nghiệm bội lẻ:
\(f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x^2+x=-1\left(vô-nghiệm\right)\\x^2+x=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Với \(\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\) \(\Rightarrow x^2+x\ge2\) ; với \(-2\le x\le1\Rightarrow-1\le x^2+x\le2\) nên ta có bảng xét dấu:

Từ BBT ta có: \(x=-\dfrac{1}{2}\) là cực đại, \(x=-2;x=1\) là 2 cực tiểu
Hàm đồng biến trên ... bạn tự kết luận
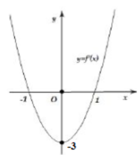
Cho hàm số y=f(x)= a x 3 + b x 2 + c x + d , ( a , b , c , d ∈ R , a khác 0) có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y= f ' ( x ) cho bởi hình vẽ dưới đây. Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giời hạn bởi đồ thị (C) và trục hoành xung quanh trục hoành Ox
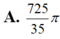
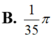
![]()
![]()
Cho hàm số
f(x)= 3 x + a - 1 khi x ≤ 0 1 + 2 x - 1 x khi x > 0
Tìm tất cả giá trị thực của a để hàm số đã cho liên tục trên R
A. a=1
B. a=3
C. a=4
D. a=2
Cho hàm số y = a x 3 + c x + d , a ≠ 0 có m i n x ∈ - ∞ ; 0 f ( x ) = f ( - 2 ) . Giá trị lớn nhất của hàm số y = f(x) trên đoạn [1;3] bằng
A. d - 11a
B. d - 16a
C. d + 2a
D. d + 8a
Chọn B
Vì y = a x 3 + c x + d , a ≠ 0 là hàm số bậc ba và có m i n x ∈ - ∞ ; 0 f ( x ) = f ( - 2 ) nên a < 0 và y' = 0 có hai nghiệm phân biệt.
Ta có ![]() có hai nghiệm phân biệt
⇔
ac < 0
có hai nghiệm phân biệt
⇔
ac < 0
Vậy với a < 0, c > 0 thì y' = 0 có hai nghiệm đối nhau 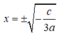
Từ đó suy ra
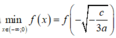
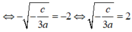
⇔
c = -12a
Ta có bảng biến thiên
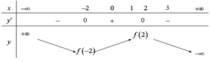
Ta suy ra ![]()
Hàm số y = a x 3 + b x 2 + c x + d đồng biến trên R khi và chỉ khi
A. a = b = 0 , c > 0 a > 0 , b 2 − 3 a c ≥ 0
B. a = b = 0 , c > 0 a < 0 , b 2 − 3 a c ≤ 0
C. a = b = 0 , c > 0 a > 0 , b 2 − 3 a c ≤ 0
D. a > 0 , b 2 − 3 a c ≤ 0
Đáp án C
Ta có y ' = 3 a x 2 + 2 b x + c
Hàm số đồng biến trên ℝ ⇔ y ' ≥ 0 , ∀ x ∈ ℝ
T H 1 : a = 0 ⇒ y ' = 2 b x + c ⇒ b = 0 ⇒ y ' = c > 0 ⇔ c > 0 b ≠ 0 ⇒ y ' = 2 b x + c ≥ 0 ⇔ c ≥ − c 2 b ⇒ a = b = 0 , c = 0 T H 2 : a ≠ 0 ⇒ y ' ≥ 0 , ∀ x ∈ ℝ ⇔ a > 0 Δ = 2 b 2 − 12 a c ≤ 0 ⇔ a > 0 b 2 − 3 a c ≤ 0
Kết hợ 2TH, ta có a = b = 0 , c > 0 a > 0 , b 2 − 3 a c ≤ 0