1. Tìm Min, Max:
a. \(7x^2-20x+y^2-4y-4xy+11\)
b. \(9x^2-12+3y^2-6xy+3\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Phân tích mỗi đa thức sau thành nhân tử
a)x^3-2x^2y+xy^2+xy
b)x^3+4x^2y+4xy^2-9x
c)x^3-y^3+x-y
d)4x^2-4xy+2x-y+y^2
e)9x^2-3x+2y-4y^2
f)3x^2-6xy+3y^2-5x+5y
a) Xem lại đề
b) x³ - 4x²y + 4xy² - 9x
= x(x² - 4xy + 4y² - 9)
= x[(x² - 4xy + 4y² - 3²]
= x[(x - 2y)² - 3²]
= x(x - 2y - 3)(x - 2y + 3)
c) x³ - y³ + x - y
= (x³ - y³) + (x - y)
= (x - y)(x² + xy + y²) + (x - y)
= (x - y)(x² + xy + y² + 1)
d) 4x² - 4xy + 2x - y + y²
= (4x² - 4xy + y²) + (2x - y)
= (2x - y)² + (2x - y)
= (2x - y)(2x - y + 1)
e) 9x² - 3x + 2y - 4y²
= (9x² - 4y²) - (3x - 2y)
= (3x - 2y)(3x + 2y) - (3x - 2y)
= (3x - 2y)(3x + 2y - 1)
f) 3x² - 6xy + 3y² - 5x + 5y
= (3x² - 6xy + 3y²) - (5x - 5y)
= 3(x² - 2xy + y²) - 5(x - y)
= 3(x - y)² - 5(x - y)
= (x - y)[(3(x - y) - 5]
= (x - y)(3x - 3y - 5)
Bài 1. Phân tích các đa thức sau thành nhân tử a) y - 9 - x + 6x b) 25 - 4x? - 4xy - y c) x - xz + 4y - 2yz + 4xy d) 3x + 6xy - 48z + 3y? e) x - z + 4y - 4t - 4xy + 4zt f) +2x'y+xy-16x Bài 2. Tìm x biết a) 3x(-3)-4x+12 -0 b) -5x=0 c) (a-2 -(x+2 =0 d) -9-4x+3)=0 Bài 3. Tính nhanh giá trị biểu thức a) A= x - 4z? - 2xy + y với x = -16; y = -6; z = 45 b) B = x - y + 2y-1 với x = 75; y = 26. c) C = 2x + xy - x'y - 2y với x= y =
giúp e làm vs ạ em đang cần gấp
bạn viết lại đề đi, có số mũ, xuống dòng chứ thế này ai mà giải được
Bài 1: Tìm gtln của các bth
a)A= -x^2 – 4x -2
b)B= -2x^2 – 3x +5
c)C= (2-x)(x + 4)
d)D= -8x^2 + 4xy – y^2 +3
Bài 2:CMR: Giá trị của các biểu thức sau luôn dương với mọi giá trị của biến
a)A=25x^2 – 20x + 7
b)B=9x^2 – 6xy + 2y^2 + 1
c)E=x^2 – 2x + y^2 – 4y +6
Bài 1:
a) Ta có: \(A=-x^2-4x-2\)
\(=-\left(x^2+4x+2\right)\)
\(=-\left(x^2+4x+4-2\right)\)
\(=-\left(x+2\right)^2+2\le2\forall x\)
Dấu '=' xảy ra khi x=-2
b) Ta có: \(B=-2x^2-3x+5\)
\(=-2\left(x^2+\dfrac{3}{2}x-\dfrac{5}{2}\right)\)
\(=-2\left(x^2+2\cdot x\cdot\dfrac{3}{4}+\dfrac{9}{16}-\dfrac{49}{16}\right)\)
\(=-2\left(x+\dfrac{3}{4}\right)^2+\dfrac{49}{8}\le\dfrac{49}{8}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{3}{4}\)
c) Ta có: \(C=\left(2-x\right)\left(x+4\right)\)
\(=2x+8-x^2-4x\)
\(=-x^2-2x+8\)
\(=-\left(x^2+2x-8\right)\)
\(=-\left(x^2+2x+1-9\right)\)
\(=-\left(x+1\right)^2+9\le9\forall x\)
Dấu '=' xảy ra khi x=-1
Bài 2:
a) Ta có: \(=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)
b) Ta có: \(B=9x^2-6xy+2y^2+1\)
\(=9x^2-6xy+y^2+y^2+1\)
\(=\left(3x-y\right)^2+y^2+1>0\forall x,y\)
c) Ta có: \(E=x^2-2x+y^2-4y+6\)
\(=x^2-2x+1+y^2-4y+4+1\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+1>0\forall x,y\)
Bài 1:Tính:
a) (2x-y)+(2x-y)+(2x-y)+3y
b) (x+2y)+(x-2y)+(8x-3y)
c) (x+2y)-2(x-2y)-(2x-3y)
Bài 2: Cho 2 đa thức P= 9x²-6xy+3y² và Q= -3x²+7xy-2y²
Tìm đa thức M biết M+2(x²-4y²)+Q=6x²-4xy+5y²+P
Bài 1:
a) (2x - y) + (2x - y) + (2x - y) + 3y
= 3(2x - y) + 3y
= 3(2x - y + 3y)
= 3(2x + 2y)
= 3.2(x + y)
= 6(x + y)
b) (x + 2y) + (x - 2y) + (8x - 3y)
= x + 2y + x - 2y + 8x - 3y
= 9x - 3y
= 3(3x - y)
c) (x + 2y) - 2(x - 2y) - (2x - 3y)
= x + 2y - 2x + 4y - 2x + 3y
= 9y - 3x
= 3(3y - x)
Bài 2:
M + 2(x2 - 4y2) + Q = 6x2 - 4xy + 5y2 + P
M + 2x2 - 8y2 -3x2 + 7xy - 2y2 = 6x2 - 4xy + 5y2 + 9x2 - 6xy + 3y2
M + 2x2 - 3x2 - 6x2 - 9x2 - 8y2 - 2y2 - 5y2 - 3y2 + 7xy + 4xy + 6xy = 0
M - 16x2 - 18y2 + 17xy = 0
M = 16x2 + 18y2 - 17xy
Tìm max hoặc min của A= -2x^2-8x+1
B=3x^2+3x-1
C=7x-2x^2+3
D=-4xy+4x-y^2-5x^2+3
\(B=3x^2+3x-1\)
\(=3\left(x^2+x-\dfrac{1}{3}\right)\)
\(=3\left(x^2+x+\dfrac{1}{4}-\dfrac{7}{12}\right)\)
\(=3\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}>=-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)
\(C=-2x^2+7x+3\)
\(=-2\left(x^2-\dfrac{7}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{73}{16}\right)\)
\(=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{73}{8}< =\dfrac{73}{8}\forall x\)
Dấu '=' xảy ra khi x-7/4=0
=>x=7/4
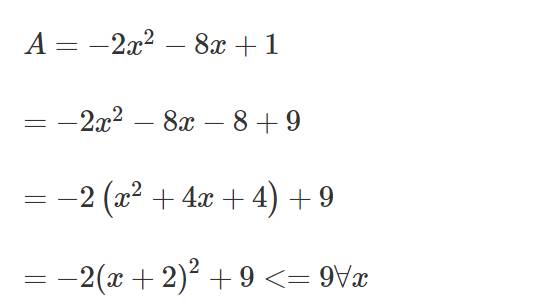
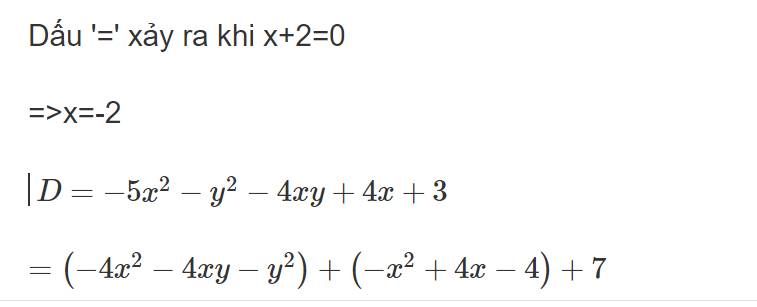
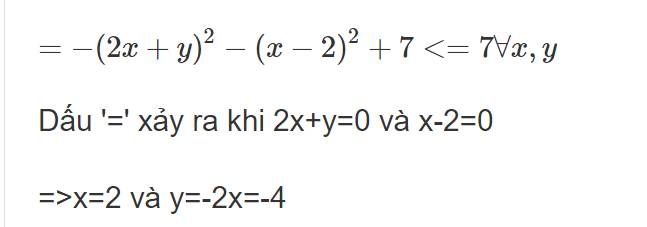
Cho 3x^2-4xy+3y^2=25 và a,b>0
Tìm min,max P=x^2+y^2
Ta có:\(3x^2-4xy+3y^2=25\)
\(\Leftrightarrow2x^2-4xy+2y^2+x^2+y^2=25\)
\(\Leftrightarrow2\left(x-y\right)^2+x^2+y^2=25\Leftrightarrow x^2+y^2=25-2\left(x-y\right)^2\le25\)
\(\Rightarrow\)GTLN của P là 25 đạt được khi x=y\(\Rightarrow3x^2-4x^2+3x^2=25\Rightarrow2x^2=25\Rightarrow x=\frac{5}{\sqrt{2}}=y\)
Lại có:\(3x^2-4xy+3y^2=25\Leftrightarrow3\left(x^2+y^2\right)=25+4xy\)
\(\Leftrightarrow3\left(x^2+y^2\right)+2\left(x^2+y^2\right)=25+2x^2+4xy+2y^2\)
\(\Leftrightarrow5\left(x^2+y^2\right)=25+2\left(x+y\right)^2\ge25\)
\(\Rightarrow x^2+y^2\ge5\)
\(\Rightarrow\)GTNN của P là 5 đạt được khi \(x=-y\Rightarrow3x^2+4x^2+3x^2=25\Rightarrow10x^2=25\Rightarrow x^2=\frac{5}{2}\Rightarrow x=\sqrt{\frac{5}{2}}\)
\(\Rightarrow y=-\sqrt{\frac{5}{2}}\)
a) 3x 2 (2x 3 – x + 5)
b) (4xy + 3y – 5x)x 2 y
c) (3x 2 y – 6xy + 9x)(- 3
4
xy)
d) - 3
1
xz(- 9xy + 15yz) + 3x 2 (2yz 2 – yz)
e) (x 3 + 5x 2 – 2x + 1)(x – 7)
f) (2x 2 – 3xy + y 2 )(x + y)
g) (x – 2)(x 2 – 5x + 1) – x(x 2 + 11)
h) [(x 2 – 2xy + 2y 2 )(x + 2y) - (x 2 + 4y 2 )(x – y)] 2xy
Mọi người giúp em với ạ
Đề bài là gì sao không ghi rõ??
y^2-9-x^2+6x
25-4x^2-4xy-y^2
x^2-xz+4y^2-2yz+4xy
3x^2+6xy-48z^2+3y^2
x^2-z^2+4y^2-4t^2-4xy+4zt
x^3+2x^2y+xy^2-16x
f(x)=(2x-3)^2+(x+4)^2-(3x^2+5x-2) tìm GTNN
F=2x^2+3y^2-8x+24y-7 tìm GTNN
F=-5x^2-4y^2+20x-32y+9 tìm GTLN
F=x^2+y^2-x+y-3 tìm GTNN
F=F=5x^2+y^2-4xy-6x+20 tìm GTNN
F=-13x^2-4y^2+12xy+20x+37
F=5x^2+9y^2-12xy+24x-48y+100
Cho x+y=5 Cho A= x^3+y^3-8(x^2+y^2)+xy+2 tính GTLN của A
Cho x+y+2=0 Tìm min của B=2(x^3+y^3)-15xy+7
Cho x+y+2=0 tìm min của C=x^4+y^4-(x^3+y^3)+2x^2y^2+2xy(x^2+y^2)+13xy