 làm hết hộ nha
làm hết hộ nha
HH
Những câu hỏi liên quan
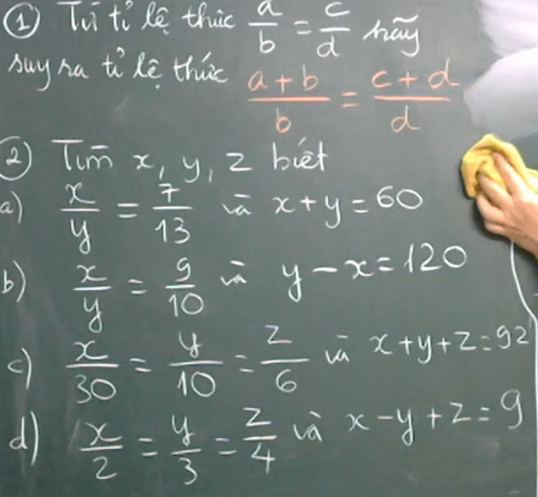
Làm hết hộ em nha!!!
Bài 2:
a) \(\dfrac{x}{y}=\dfrac{7}{13}\Rightarrow\dfrac{x}{7}=\dfrac{y}{13}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=\dfrac{60}{20}=3\)
\(\dfrac{x}{7}=3\Rightarrow x=21\\ \dfrac{y}{13}=3\Rightarrow y=39\)
b) \(\dfrac{x}{y}=\dfrac{9}{10}\Rightarrow\dfrac{x}{9}=\dfrac{y}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{9}=\dfrac{y}{10}=\dfrac{y-x}{10-9}=120\)
\(\dfrac{x}{9}=120\Rightarrow x=1080\\ \dfrac{y}{10}=120\Rightarrow y=1200\)
c) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{30}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x+y+z}{30+10+6}=\dfrac{92}{46}=2\)
\(\dfrac{x}{30}=2\Rightarrow x=60\\ \dfrac{y}{10}=2\Rightarrow y=20\\ \dfrac{z}{6}=2\Rightarrow z=12\)
d)Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x-y+z}{2-3+4}=\dfrac{9}{3}=3\)
\(\dfrac{x}{2}=3\Rightarrow x=6\\ \dfrac{y}{3}=3\Rightarrow y=9\\ \dfrac{z}{4}=3\Rightarrow z=12\)
Đúng 2
Bình luận (0)
Bài 1:
\(\dfrac{a+b}{b}=\dfrac{a}{b}+1\)
\(\dfrac{c+d}{d}=\dfrac{c}{d}+1\)
Mà \(\dfrac{a}{b}=\dfrac{c}{d};1=1\Rightarrow\dfrac{a}{b}+1=\dfrac{c}{d}+1\Rightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Làm hộ mik nha . Nhanh chút !! Giải hết câu này nha
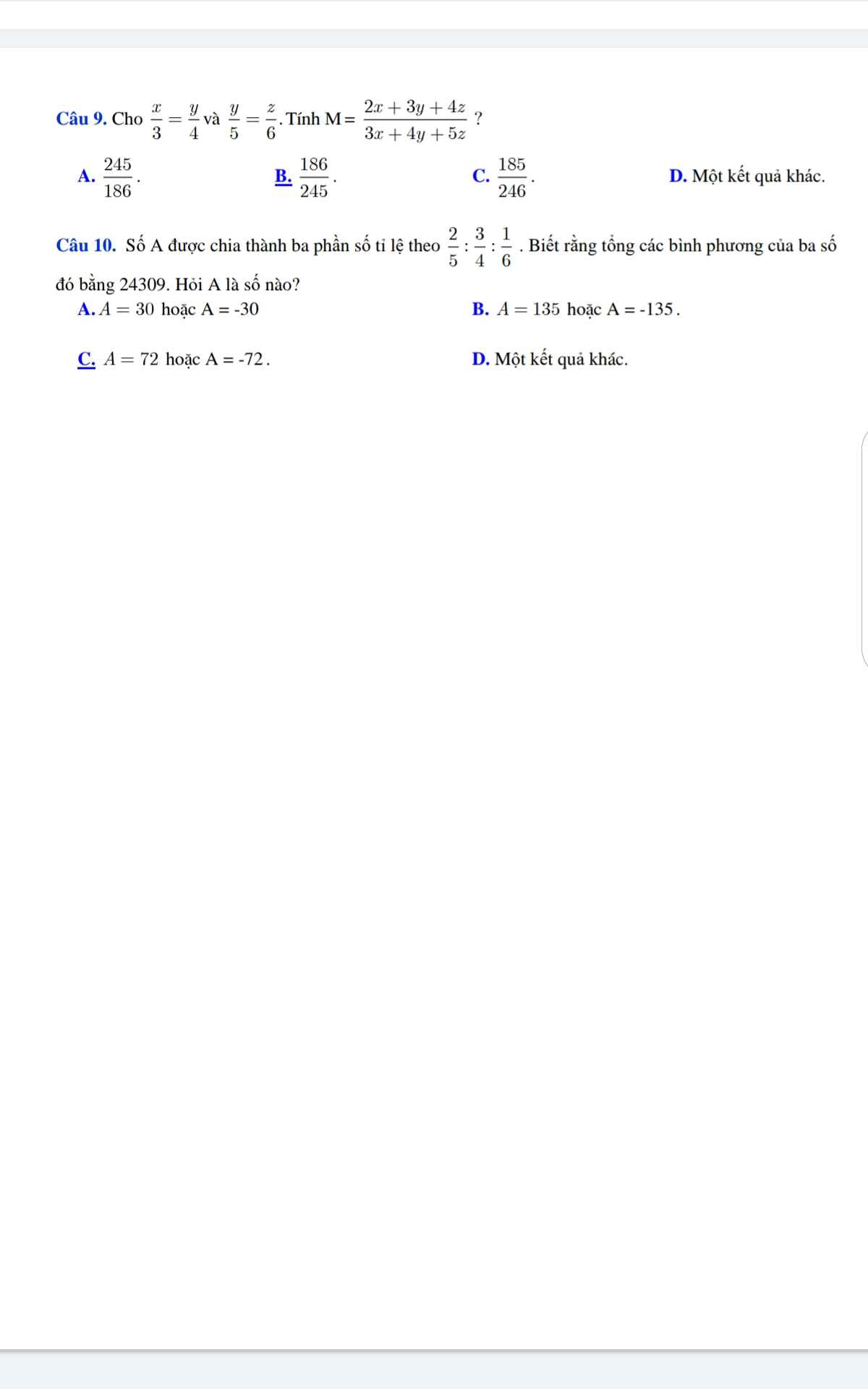
Câu 9 cần bs điều kiện $x,y,z\neq 0$
$\frac{x}{3}=\frac{y}{4}\Rightarrow \frac{x}{15}=\frac{y}{20}$
$\frac{y}{5}=\frac{z}{6}\Rightarrow \frac{y}{20}=\frac{z}{24}$
$\Rightarrow \frac{x}{15}=\frac{y}{20}=\frac{z}{24}$ và đặt $=t$ (đk: $t\neq 0$)
$\Rightarrow x=15t; y=20t; z=24t$
Khi đó:
$M=\frac{2.15t+3.20t+4.24t}{3.15t+4.20t+5.24t}=\frac{186t}{245t}=\frac{186}{245}$
Đáp án B.
Đúng 1
Bình luận (3)
Câu 10:
Giả sử số $A$ được chia thành 3 phần $a,b,c$ sao cho
$a:b:c=\frac{2}{5}: \frac{3}{4}: \frac{1}{6}$
Đặt $a=\frac{2}{5}t; b=\frac{3}{4}t; c=\frac{1}{6}t$
$A=a+b+c=\frac{2}{5}t+\frac{3}{4}t+\frac{1}{6}t=\frac{79}{60}t$
Có:
$a^2+b^2+c^2=(\frac{2}{5}t)^2+(\frac{3}{4}t)^2+(\frac{1}{6}t)^2=24309$
$t^2=32400$
$t=\pm 180$
$\Rightarrow A=\frac{79}{60}t=\frac{79}{60}\pm 180=\pm 237$
Đáp án D.
Đúng 1
Bình luận (0)
 Làm hộ em vs ạ:'((, hết luôn nha
Làm hộ em vs ạ:'((, hết luôn nha

phần I là đc nha mn zui tính thì làm hết hộ mình nha

Làm hết hộ em nha, em cảm ơn ạ!

Làm hết hộ em nha em xin cảm ơn ạ
Bạn thể tự viết ra bởi vì mỗi người có những ý kiến khác nhau
Đúng 0
Bình luận (0)
Làm hết hộ em nha, em cảm ơn nhiều ạ!!

Bạn nào biết làm hộ mik được ko ạ! Mik cảm ơn! Bạn nào làm hộ mik, mik tick hết chứ ko phải mỗi bn đầu! Bạn nào biết bài nào thì làm hộ mik bài đó nha!
#include <bits/stdc++.h>
using namespace std;
double a,b,c,p,s;
int main()
{
cin>>a>>b>>c;
p=(a+b+c)/2;
s=sqrt(p*(p-a)*(p-b)*(p-c));
cout<<fixed<<setprecision(2)<<p;
return 0;
}
Đúng 0
Bình luận (0)
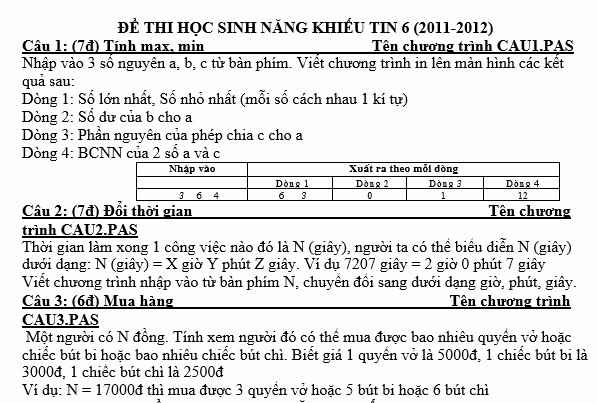
Bạn nào biết làm hộ mik được ko ạ! Mik cảm ơn! Bạn nào làm hộ mik, mik tick hết chứ ko phải mỗi bn đầu! Bạn nào biết bài nào thì làm hộ mik bài đó nha!
1:
uses crt;
var a,b,c,max,min:longint;
begin
clrscr;
readln(a,b,c);
max=a;
if max<b then max:=b;
if max<c then max:=c;
min:=a;
if min>c then min:=c;
if min>b then min:=b;
writeln(max,' ',min);
readln;
end.
Đúng 1
Bình luận (1)
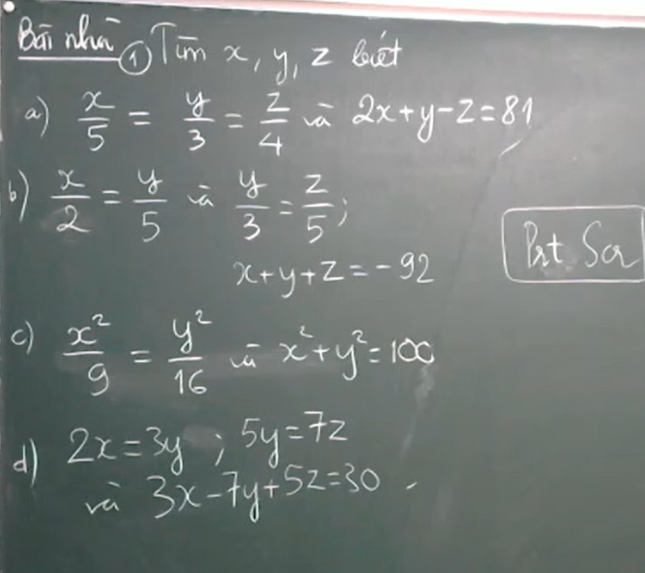
Làm hết hộ em nha em cảm ơn mọi người ạ
a) Ta có:
\(\dfrac{x}{5}=\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2x+y-z}{10+3-4}=\dfrac{81}{9}=9\\ \Rightarrow\left\{{}\begin{matrix}x=9\cdot5=45\\y=9\cdot3=27\\z=9\cdot4=36\end{matrix}\right.\)
Vậy x = 45; y = 27; z = 36.
b) Ta có:
\(\dfrac{x}{2}=\dfrac{y}{5}\)\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{15}\)
\(\dfrac{y}{3}=\dfrac{z}{5}\)\(\Rightarrow\dfrac{y}{15}=\dfrac{z}{25}\)
suy ra, \(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}=\dfrac{x+y+z}{6+15+25}=-\dfrac{92}{46}=-2\\
\Rightarrow\left\{{}\begin{matrix}x=-2\cdot6=-12\\y=-2\cdot15=-30\\z=-2\cdot25=-50\end{matrix}\right.\)
Vậy x = -12; y = -30; z = -50.
c) Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=4\\ \Rightarrow\left\{{}\begin{matrix}x^2=36\\y^2=64\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=6\\y=8\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=8\end{matrix}\right.\\\left\{{}\begin{matrix}x=6\\y=-8\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=-8\end{matrix}\right.\end{matrix}\right.\)
Vậy (x; y) \(\in\left\{\left(6;8\right);\left(-6;8\right);\left(6;-8\right);\left(-6;-8\right)\right\}\)
d), Ta có:
\(2x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\Rightarrow\dfrac{x}{21}=\dfrac{y}{14}\\ 5y=7z\Rightarrow\dfrac{y}{7}=\dfrac{z}{5}\Rightarrow\dfrac{y}{14}=\dfrac{z}{10}\\ \Rightarrow\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\\ \Rightarrow\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}=\dfrac{3x-7y+5z}{63-98+50}=\dfrac{30}{15}=2\\
\Rightarrow\left\{{}\begin{matrix}x=2\cdot21=42\\y=2\cdot14=28\\z=2\cdot10=20\end{matrix}\right.\)
Vậy x = 42; y = 28; z = 20.
Đúng 1
Bình luận (0)
a: Ta có: \(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{4}\)
nên \(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2x+y-z}{10+3-4}=\dfrac{81}{9}=9\)
Do đó: x=45; y=27; z=36
b: Ta có: \(\dfrac{x}{2}=\dfrac{y}{5}\)
nên \(\dfrac{x}{6}=\dfrac{y}{15}\left(1\right)\)
Ta có: \(\dfrac{y}{3}=\dfrac{z}{5}\)
nên \(\dfrac{y}{15}=\dfrac{z}{25}\left(2\right)\)
Từ (1), (2) suy ra \(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}\)
mà x+y+z=-92
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}=\dfrac{x+y+z}{6+15+25}=-\dfrac{92}{46}=-2\)
Do đó: x=-12; y=-30; z=-50
c: Ta có: \(\dfrac{x^2}{9}=\dfrac{y^2}{16}\)
mà \(x^2+y^2=100\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
Do đó: \(\left\{{}\begin{matrix}x^2=36\\y^2=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{6;-6\right\}\\y\in\left\{8;-8\right\}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
d: Ta có: 2x=3y
nên \(\dfrac{x}{3}=\dfrac{y}{2}\)
hay \(\dfrac{x}{21}=\dfrac{y}{14}\left(1\right)\)
Ta có: 5y=7z
nên \(\dfrac{y}{7}=\dfrac{z}{5}\)
hay \(\dfrac{y}{14}=\dfrac{z}{15}\left(2\right)\)
Từ (1), (2) suy ra \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{15}\)
hay \(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{75}\)
mà 3x-7y+5z=30
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{75}=\dfrac{3x-7y+5z}{63-98+75}=\dfrac{30}{40}=\dfrac{3}{4}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{63}{4}\\y=\dfrac{21}{2}\\z=\dfrac{45}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (0)







