Cho hình 69 trong đó \(AE\perp BC\)
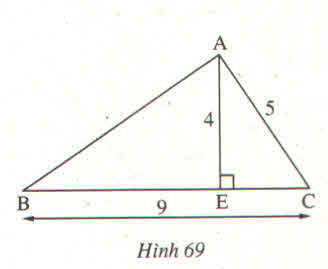
Tính AB biết AE = 4m, AC = 5m, BC = 9m
Cho hình dưới trong đó AE ⊥BC. Tính AB biết AE = 4m; AC = 5m; BC = 9m
Áp dụng định lý pitago vào tam giác vuông AEC ta có:
AC2=AE2+EC2
=>EC2=AC2-AE2=52-42=25-16=9
=>EC=3M
Ta có: BC = BE + EC
BE = BC – EC = 9 – 3 = 6(m)
Áp dụng định lí pitago vào tam giác vuông AEB, ta có:
AB2=AE2+EB2=42+62=16+36=52
Suy ra: AB = √52(m) ≈7,2m
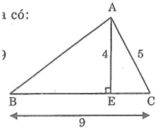
Cho tam giác nhọn ABC. Kẻ AE vuông góc với BC, biết AC=5m, AE=4m và BC=9m
a) Tính độ dài EC, BE, AB
b) Tính chu vi tam giác ABC
a) Áp dụng định lí Pytago vào ΔAEC vuông tại E, ta được:
\(AC^2=AE^2+EC^2\)
\(\Leftrightarrow EC^2=AC^2-AE^2=5^2-4^2=9\)
hay EC=3(cm)
Vậy: EC=3cm
Ta có: BE+EC=BC(E nằm giữa B và C)
nên BE=BC-EC=9-3=6(cm)
Vậy: BE=6cm
Áp dụng định lí Pytago vào ΔABE vuông tại E, ta được:
\(AB^2=AE^2+BE^2\)
\(\Leftrightarrow AB^2=6^2+4^2=52\)
hay \(AB=2\sqrt{13}cm\)
Vậy: \(AB=2\sqrt{13}cm\)
b) Chu vi của tam giác ABC là:
\(AB+AC+BC=2\sqrt{13}+5+9=14+2\sqrt{13}cm\)
cho hình trong đó AE vuông BC . tính AB biết AE =4cm,AC=5cm , Bc=9cm
Cho hình thang ABCD trong đó D thuộc AB; E thuộc AC; DE//BC; biết AD=18cm, DB=12cm; AE=30cm. Tính độ dài AC
4. Cho tam giác ABC có AB = AC, kẻ tia phân giác góc A cắt BC tại E. CMR:
ΔAEB = ΔAEC từ đó suy ra \(AE\perp BC\).
Để chứng minh ΔAEB = ΔAEC, ta có thể sử dụng nguyên lý cắt giao. Vì AB = AC và AE là tia phân giác góc A, nên ta có AE là đường trung trực của đoạn thẳng BC. Từ đó, ta có AE ⊥ BC. Vì AE là đường trung trực của đoạn thẳng BC, nên ta cũng có BE = EC. Như vậy, ta đã chứng minh được ΔAEB = ΔAEC.
Cho tam giác \(ABC\), biết \(DE//BC\) (Hình 2). Trong các khẳng định sau, khẳng định nào sai?
A. \(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\).
B. \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\).
C. \(\frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).
D. \(\frac{{BD}}{{AB}} = \frac{{DE}}{{BC}}\).
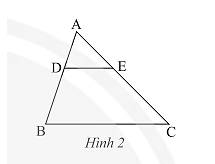
Vì \(DE//BC\) nên theo định lí Thales và hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}};\frac{{BD}}{{AD}} = \frac{{EC}}{{AE}};\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}};\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).
Bài 1: Cho tam giác ABC có \(\widehat{A}\)\(=90^o\) Vẽ AD \(\perp\)AB ( D,C nằm khác phía đối với AB) và AD=AB. Vẽ AE \(\perp\)AC ( E,B nằm khác phía đối với AC) và AE=AC. Biết DE=BC. Tính \(\widehat{BAC}\)
Bài 2:Cho tam giác ABC có AB=AC. Kẻ AE là phân giác của \(\widehat{BAC}\)( E thuộc BC). Chứng minh rằng:
a) \(\Delta ABE=\Delta ACE\)
b) AE là đường trung trực của đoạn thẳng BC
cho ΔABC có góc A tù. Kẻ AD⊥AB và AB = AD ( tia AD nằm giữa hai tia AB và AC). Kẻ AE ⊥ AC và AE = AC ( tia AE nằm giữa hai tia AB và AC). Gọi M là trung điểm của BC. Chứng minh rằng AM ⊥ DE
Cho tam giác ABC vuông tại A, đường cao AH( H thuộc BC). Từ H kẻ HE\(\perp\)AC, HF\(\perp\)AB, AB=c, AC=b.
a) tính AE, AF theo b,c
b)CM: BF\(\sqrt{CH}+CE\sqrt{BH}=AH\sqrt{BC}\)