Cho hình bs.4.
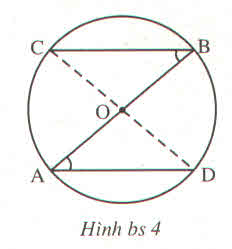
Chứng minh rằng :
a) C, O, D thẳng hàng
b) BC = AD
Cho hình bs 4. Chứng minh rằng :
C,O,D thẳng hàng
+) Xét tam giác OAD có: OA = OD (= bán kính đường tròn)
Suy ra tam giác OAD cân tại O.
Suy ra: ∠A = ∠D ( tính chất tam giác cân). (1)
+) Xét tam giác OBC có: OB = OC (= bán kính đường tròn)
Suy ra tam giác OBC cân tại O.
Suy ra: ∠B = ∠C ( tính chất tam giác cân). (2)
+) Lại có: ∠A = ∠B ( giả thiết) (3)
Từ (1); (2) và (3) suy ra: ∠A = ∠B = ∠C = ∠D
Vậy hai tam giác cân OAD và OBC có góc ở đáy bằng nhau nên góc ở đỉnh bằng nhau: ∠AOD = ∠BOC (4).
+) Ta có: ∠AOD + ∠DOB = 180º ( hai góc kề bù) (5)
Từ (4) và (5) suy ra: ∠BOC + ∠DOB = 180º hay 3 điểm C, O và D thẳng hàng.
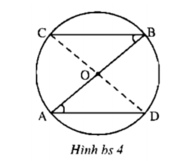
Cho hình bs 4. Chứng minh rằng :
BC = AD
Xét tam giác OAD và ∆ OCB có:
OA = OC ( = bán kính đường tròn)
∠AOD = ∠BOC ( hai góc đối đỉnh)
OD = OB ( = bán kính đường tròn)
Suy ra:∆ OAD = ∆ OCB ( c.g.c)
Suy ra: AD = BC ( hai cạnh tương ứng).
Cho 4 điểm A,B,C,D biết AB= 3cm, BC= 2cm, AC= 5cm, CD= 1cm, AD= 6cm. Chứng minh rằng A,B,C,D thẳng hàng.
Có: CD = 1cm => C, D thẳng hàng
AC = 5cm => A, C thẳng hàng
AB = 3cm => A,B thẳng hàng
BC = 2cm => B , C thẳng hàng
AD = 6cm => A,D thẳng hàng
Vậy A, B , C , D thẳng hàng
Cho hình thang cân ABCD(AB//CD), AB=BC và BC vuông góc với BD
a) Chứng minh AC vuông góc với AD
b) Tính số đo các góc hình thang
c) Gọi O là giao điểm của 2 đường chéo. Chứng minh rằng O cách đều 2 cnhj bên và đáy lớn
d) Gọi M là giao điểm cảu AD và Bc. H là hình chiếu của O trên DC. Chứng minh M,H,O thẳng hàng
cho 4 điểm A, B, C, D và đường thẳng xy. Biết rằng AB vuông góc với xy, BC vuông góc với xy, AD vuông góc với xy. Chứng minh 4 điểm A, B, C, D thẳng hàng
cho hình vẽ: a)chứng minh AE//BC và AD//BC b)chứng minh A,E,D thẳng hàng 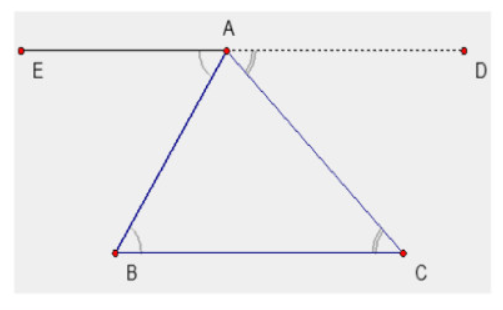
a: Ta có: \(\widehat{EAB}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
Ta có: \(\widehat{DAC}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
b: Ta có: AE//BC
AD//BC
mà AD và AE có điểm chung là A
nên D,A,E thẳng hàng
Cho hình 88.
a) Hãy xác định vị trí tương đối của hai đường tròn (O) và (O’).
b) Chứng minh rằng BC // OO’ và ba điểm C, B, D thẳng hàng.
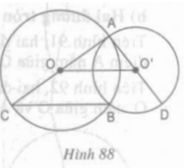
a) Hai đường tròn (O) và (O’) cắt nhau
b) Xét tam giác ABC có:
OA = OB = OC = bán kính đường tròn (O)
Mà BO là trung tuyến của tam giác ABC
⇒ ∆ABC vuông tại B ⇒ AB ⊥ BC (1)
Lại có OO’ là đường trung trực của AB
⇒ AB ⊥ OO' (2)
Từ (1) và (2) ⇒ OO’ // BC
Chứng minh tương tự ta có ∆ABD vuông tại B ⇒ AB ⊥ BD (3)
Từ (1) và (3) ⇒ B, C, D thẳng hàng.
Cho hình thang ABCD (AB//CD), biết AD+BC=AB. Hai tia phân giác của hai góc C và D cắt nhau tại E. Chứng minh rằng 3 điểm A,B,E thẳng hàng