mọi người làm giúp em câu c với ạ
em đang cần gấp ạ
MỌI NGƯỜI GIÚP EM VỚI Ạ (EM ĐANG CẦN NÓ GẤP AÁY Ạ AI LÀM ĐƯỢC CÂU NÀO THÌ GIÚP EM CÂU ĐÓ NHÉ)
EM CẢM ƠN Ạ 
Câu 7:
a, \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
\(CuO+H_2SO_4\rightarrow CuSO_4+H_2O\)
b, \(n_{H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
Theo PT: \(n_{Fe}=n_{H_2}=0,1\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Fe}=\dfrac{0,1.56}{10}.100\%=56\%\\\%m_{CuO}=44\%\end{matrix}\right.\)
c, \(n_{CuO}=\dfrac{10-0,1.56}{80}=0,055\left(mol\right)\)
Theo PT: \(n_{H_2SO_4}=n_{Fe}+n_{CuO}=0,155\left(mol\right)\)
\(\Rightarrow C\%_{H_2SO_4}=\dfrac{0,155.98}{100}.100\%=15,19\%\)
d, Theo PT: \(\left\{{}\begin{matrix}n_{FeSO_4}=n_{Fe}=0,1\left(mol\right)\\n_{CuSO_4}=n_{CuO}=0,055\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m_{FeSO_4}=0,1.152=15,2\left(g\right)\\m_{CuSO_4}=0,055.160=8,8\left(g\right)\end{matrix}\right.\)
Câu 8:
a, \(CuCO_3+2HCl\rightarrow CuCl_2+CO_2+H_2O\)
b, \(n_{CO_2}=\dfrac{3,36}{22,4}=0,15\left(mol\right)\)
Theo PT: \(n_{CuCO_3}=n_{CO_2}=0,15\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{CuCO_3}=\dfrac{0,15.124}{20}.100\%=93\%\\\%m_{CuCl_2}=7\%\end{matrix}\right.\)
c, \(n_{HCl}=2n_{CO_2}=0,3\left(mol\right)\)
\(\Rightarrow C_{M_{HCl}}=\dfrac{0,3}{0,2}=1,5\left(M\right)\)
Bài 6:
a, \(SO_2+Ca\left(OH\right)_2\rightarrow CaSO_3+H_2O\)
b, \(n_{SO_2}=\dfrac{1,12}{22,4}=0,05\left(mol\right)\)
Theo PT: \(n_{Ca\left(OH\right)_2}=n_{CaSO_3}=n_{SO_2}=0,05\left(mol\right)\)
\(\Rightarrow C\%_{Ca\left(OH\right)_2}=\dfrac{0,05.74}{100}.100\%=3,7\%\)
c, \(m_{CaSO_3}=0,05.120=6\left(g\right)\)
Mọi người ơi,nếu biết làm câu nào thì giúp em với ạ,em đang cần gấp,cảm ơn mọi người trc ạ.
Câu 2.
\(C=\dfrac{N}{20}=\dfrac{4080}{20}=204\)(chu kì)
\(L=\dfrac{N}{2}\cdot3,4=\dfrac{4080}{2}\cdot3,4=6936A^o\)
\(G=X=30\%\cdot4080=1224nu\)
\(A=T=\dfrac{4080-2\cdot1224}{2}=816nu\)
\(a.C=\dfrac{N}{20}=204\)
\(b.L=\dfrac{Nx3,4}{2}=6936A\)
\(c.A=T=20\%N=816;G=X=30\%N=1224\)
\(d.rN=\dfrac{N}{2}=2040\)
b.L=Nx3,4/2=6936A
c.A=T=20%N=816;G=X=30%N=1224
làm ơn mọi người , em đang cần gấp lắm ạ . Mong mọi người giải nhanh giúp em với ạ . 
3:
a:Các tia trên hình là Ax,Ay,Bx,By,Cx,Cy
=>Có 6 tia
b: AB<AC
=>B nằm giữa A và C
=>AB+BC=AC
=>BC=4cm
c: AI=3/2=1,5cm
CI=7-1,5=5,5cm
Mọi người giúp em câu 1 với ạ trình bày chi tiết giúp em luôn ạ (em đang cần gấp)
Câu 1:
\(\left\{{}\begin{matrix}y-2x< =2\\2y-x>=4\\x+y< =5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y< =2x+2\\2y>=x+4\\y< =-x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y< =2x+2\\y< =-x+5\\y>=\dfrac{1}{2}x+2\end{matrix}\right.\)
y<=2x+2
=>y-2x-2<=0
Vẽ đường thẳng y=2x+2
Khi x=0 và y=0 thì \(y-2x-2=0-0-2=-2< =0\)(đúng)
=>Miền nghiệm của BPT y<=2x+2 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y<=-x+5
=>x+y-5<=0
Khi x=0 và y=0 thì \(x+y-5=0+0-5< =0\)(đúng)
=>Miền nghiệm của BPT y<=-x+5 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y>=1/2x+2
=>\(-\dfrac{1}{2}x+y-2>=0\)
Khi x=0 và y=0 thì \(-\dfrac{1}{2}x+y-2=-\dfrac{1}{2}\cdot0+0-2=-2< 0\)
=>O(0;0) không thỏa mãn BPT \(-\dfrac{1}{2}x+y-2>=0\)
=>Miền nghiệm của BPT \(y>=\dfrac{1}{2}x+2\) là nửa mặt phẳng chứa biên nhưng không chứa điểm O(0;0)
Vẽ đồ thị:
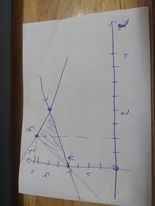
Theo hình vẽ, ta có: Miền nghiệm của hệ BPT sẽ là ΔABC, với A(0;2); B(1;4); C(2;3)
Khi x=0 và y=2 thì F=2-0=2
Khi x=1 và y=4 thì F=4-1=3
Khi x=2 và y=3 thì F=3-2=1
=>Chọn A
mọi người làm ơn giúp em với ạ em đang cần gấp
Mọi người giúp em câu 3 với ạ, em đang cần gấp lắm rồi :((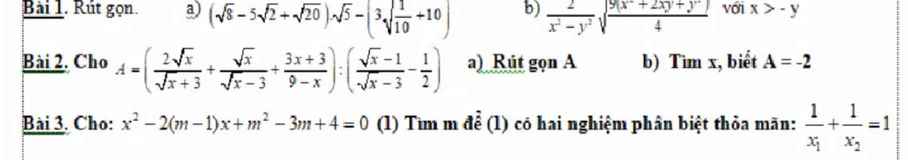
Câu 3:
\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m^2-3m+4\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-3m+4\right)\)
\(=4m^2-16m+4-4m^2+12m-16=-4m-12\)
Để phương trình có hai nghiệm phân biệt thì -4m-12>0
=>-4m>12
hay m<-3
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3m+4\end{matrix}\right.\)
Theo đề, ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow m^2-3m+4-2m+2=0\)
=>(m-2)(m-3)=0
hay \(m\in\varnothing\)
em đang cần gấp câu này lắm ạ mọi người giúp em với. em cảm ơn!
Do vai trò của 3 biến là như nhau, không mất tính tổng quát giả sử \(x>y>z\)
Ta có: \(x-z=\left(x-y\right)+\left(y-z\right)\)
Đặt \(\left\{{}\begin{matrix}x-y=a>0\\y-z=b>0\end{matrix}\right.\)
Do \(x;z\in\left[0;2\right]\Rightarrow x-z\le2\) hay \(a+b\le2\)
Ta có:
\(P=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{4}{a+b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\)
\(P\ge\dfrac{9}{\left(a+b\right)^2}\ge\dfrac{9}{2^2}=\dfrac{9}{4}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a=b\\a+b=2\\\end{matrix}\right.\) \(\Rightarrow a=b=1\) hay \(\left(x;y;z\right)=\left(0;1;2\right)\) và các hoán vị
Mọi người giải giúp em câu c và câu d với, đang cần gấp lắm ạ 😢😢😢
Mọi người giúp em hai câu này với ạ đang cần gấp