Chứng minh rằng:
Nếu {a>0; b>0 ; x,y \(\in\) R} thì \(\dfrac{x^2}{a}+\dfrac{y^2}{b}\ge\dfrac{\left(x+y\right)^2}{a+b}\)
Bài 4: Chứng minh rằng: -(a-b-c)+(-a+b-c)-(-a+b+c)=-(a-b+c)
Bài 5: Cho M=(-a+b)-(b+c-a)+(c-a) Chứng minh rằng: Nếu a<0 thì M>0
Mình cần gấp ạ!
\(4,VT=-a+b+c-a+b-c+a-b-c=-a+b-c=-\left(a-b+c\right)=VP\\ 5,M=-a+b-b-c+a+c-a=-a\\ M>0\Rightarrow-a>0\Rightarrow a< 0\)
Chứng minh rằng nếu a > 0 , b > 0 , c > 0 v à a < b thì a b < a + c b + c
Ta có: a b < a + c b + c
⇔ a(b + c) < (a + c)b
(vì a > 0, b > 0 và c > 0 ⇔ b + c > 0 và a + c > 0)
⇔ ab + ac < ab + bc
⇔ ac < bc ⇔ a < b (luôn đúng, theo gt)
Chứng minh rằng nếu a b < c d (b > 0, d > 0) thì a b < a + c b + d < c d
Áp dụng kết quả bài 5, ta có: 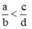 ⇒ ad < bc (1)
⇒ ad < bc (1)
Cộng cả hai vế của (1) với ab ta có: ab + ad < ab + bc
hay a(b + d) < b.(a + c)
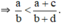
Cộng cả hai vế của (1) với cd ta có: ad + cd < bc + cd
Hay d(a + c) < c(b + d)
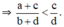
Vậy 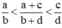
Chứng minh rằng nếu a b < c d ( b > 0 , d > 0 ) thì: a b < a + c b + d < c d
Ta có: a b < c d ⇒ a d < b c n ê n
a b + a d < a b + b c ⇔ a ( b + d ) < b ( a + c ) ⇔ a b < a + c b + d
Mặt khác:
a d + c d < b c + d c ⇔ d ( a + c ) < c ( b + d ) ⇔ a + c b + d < c d
Từ (1) và (2): a b < a + c b + d < c d
Chứng minh rằng nếu 0<a<1 thì căn a>a
Chứng minh rằng nếu 0<a<1 thì căn a > a
Chứng minh rằng: Nếu a + b b + c = c + d d + a (c + d ≠ 0) thì a = c hoặc a = b + c + d = 0
Chứng minh rằng nếu a3 +b3+c3 =3abc thì a+b+c =0 hoặc a = b= c
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b+c=0\\a=b=c\end{matrix}\right.\)
\(a^3+b^3+c^3=3abc\\ \Leftrightarrow a^3+b^3+c^3-3abc=0\\ \Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc=0\\ \Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\\ \Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a+b+c=0\\a^2+b^2+c^2-ab-bc-ca=0\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac=0\\ \Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\Leftrightarrow a=b=c\)
Vậy \(a^3+b^3+c^3=3abc\Leftrightarrow\left[{}\begin{matrix}a+b+c=0\\a=b=c\end{matrix}\right.\)
Chứng minh rằng nếu a2+b2+c2-ab-bc-ac=0 thì a=b=c
Ta có :
\(\left(a-b-c\right)^2=a^2+b^2+c^2-2ab-2bc-2ac\)
mà theo đề bài \(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-\left(ab+bc+ac\right)=0\)
mà \(-\left(ab+bc+ac\right)\le0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow dpcm\)
Chứng minh rằng nếu \(0< b< a\le2\) và \(2ab\le2b+a\) thì \(a^2+b^2\le5\)