Mọi người ơi, giúp mình mấy bài này với ^^

Giúp mình mấy bài này với mọi người ơi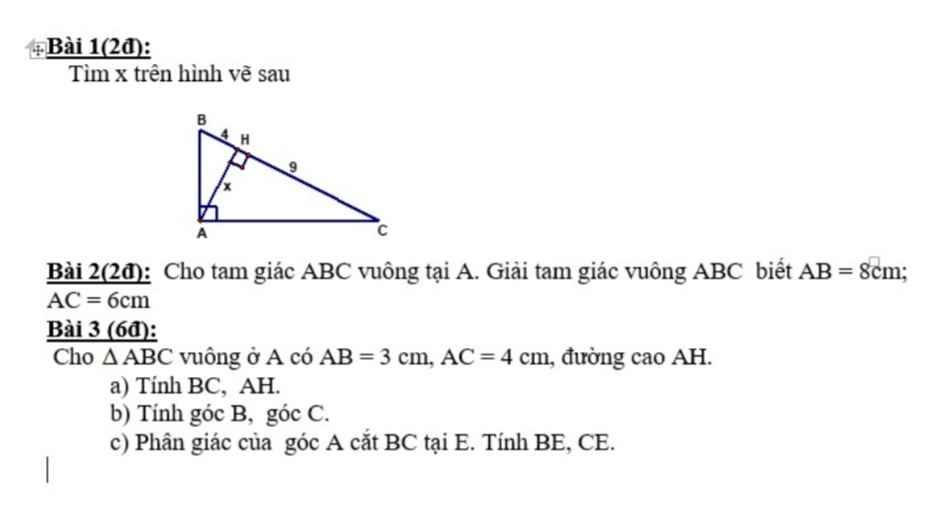
Bài 1:
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH$
$\Leftrightarrow x^2=4.9=36$
$\Rightarrow x=6$ (do $x>0$)
Bài 2:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
$\sin B=\frac{AC}{BC}=\frac{6}{10}=\frac{3}{5}$
$\Rightarrow \widehat{B}=36,87^0$
$\widehat{C}=90^0-\widehat{B}=90^0-36,87^0=53,13^0$
Bài 3:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
b.
$\sin B=\frac{AC}{BC}=\frac{4}{5}$
$\Rightarrow \widehat{B}=53,13^0$
$\widehat{C}=90^0-\widehat{B}=36,87^0$
c.
Áp dụng tính chất tia phân giác:
$\frac{BE}{CE}=\frac{AB}{AC}=\frac{3}{4}$
$\Rightarrow \frac{BE}{BC}=\frac{3}{7}$
$\Rightarrow BE=BC.\frac{3}{7}=\frac{5.3}{7}=\frac{15}{7}$ (cm)
$CE=BC-BE=5-\frac{15}{7}=\frac{20}{7}$ (cm)
Mọi người ơi giúp mình mấy bài địa này với ạ 

Mọi người ơi giúp mình mấy bài này với (bài khó quá mik làm mãi ko ra mà 8h phải nộp rồi ) giúp mik với huhu

Giúp mình mấy bài này với mọi ngừi ơi
a) \(\dfrac{2x}{3}\)+\(\dfrac{2x-1}{6}\)=4 - \(\dfrac{x}{3}\)
<=>\(\dfrac{2x}{3}\)+\(\dfrac{2x-1}{6}\) - 4+\(\dfrac{x}{3}\)=0
<=>\(\dfrac{2x.2+2x-1-4.6+x.2}{6}\)=0
=>4x-2x-24+2x=0
<=>4x-24=0
<=>4x=24
<=>x=6
Vậy x=6
b)\(\dfrac{x-1}{2}\)+\(\dfrac{x-1}{4}\)=1 - \(\dfrac{2\left(x-1\right)}{3}\)
<=>\(\dfrac{x-1}{2}\)+\(\dfrac{x-1}{4}\)-1+\(\dfrac{2\left(x-1\right)}{3}\)=0
<=>\(\dfrac{6.\left(x-1\right)+3\left(x-1\right)-1.12+4.2\left(x-1\right)}{12}\)=0
=>6x-6+3x-3-12+4x-4+2x-2=0
<=>15x-27=0
<=>15x=27
<=>x=\(\dfrac{9}{5}\)
Vậy x=\(\dfrac{9}{5}\)
d)\(\dfrac{7x}{8}\)-5(x-9)=20x+\(\dfrac{1,5}{6}\)
<=>\(\dfrac{7x}{8}\)-5(x-9)-20x-\(\dfrac{1,5}{6}\)=0
<=>\(\dfrac{3.7x-24.5\left(x-9\right)-20x.24-1,5.4}{24}\)=0
=>-478x+165=0
<=> - 478= - 165
<=> x=\(\dfrac{165}{487}\)
Vậy x =\(\dfrac{165}{487}\)
Mọi ngừi ơi giúp mình mấy bài này với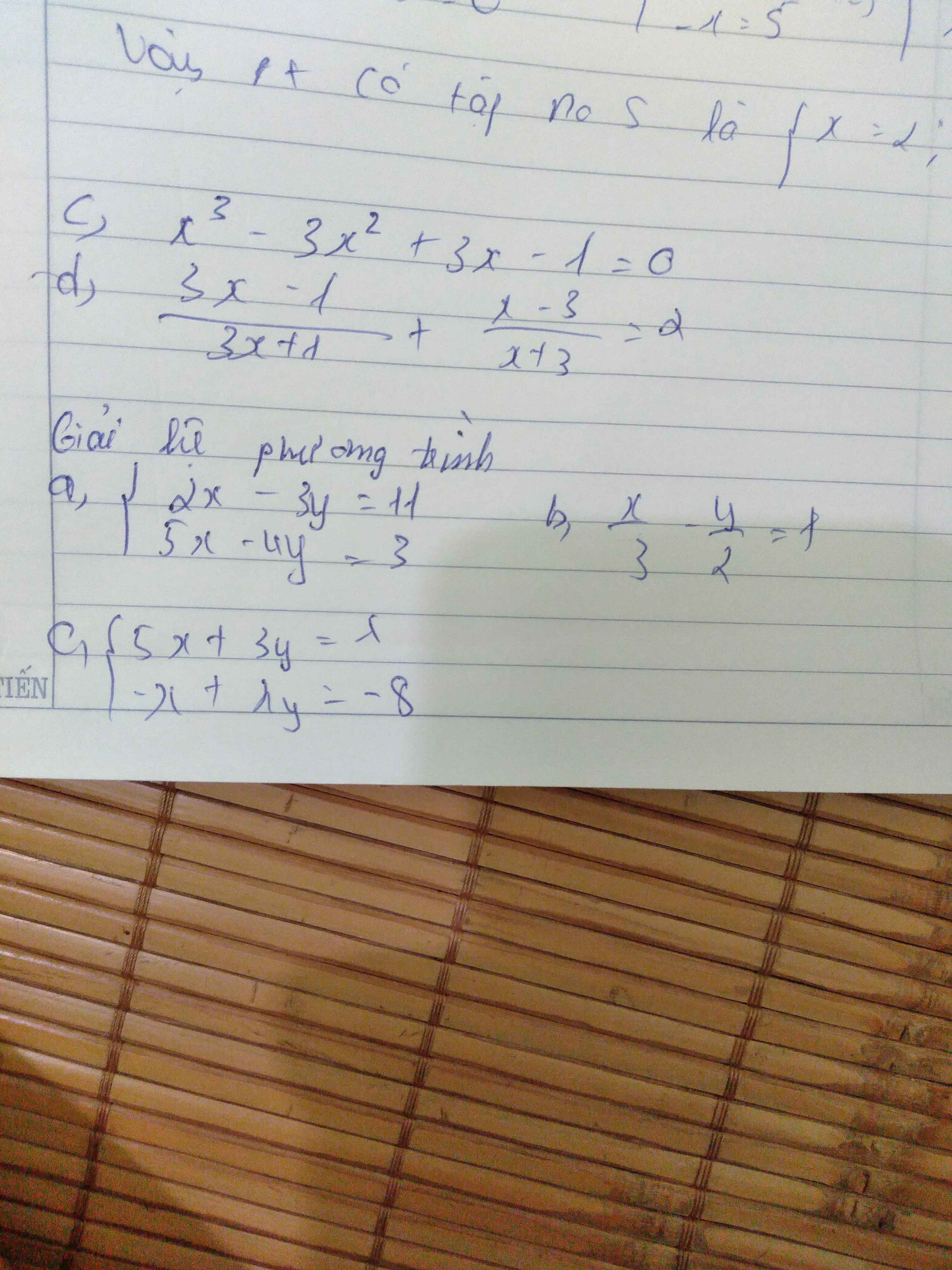
Lời giải.
c.
$x^3-3x^2+3x-1=0$
$\Leftrightarrow (x-1)^3=0$
$\Leftrightarrow x-1=0$
$\Leftrightarrow x=1$
Vậy pt có tập nghiệm $S=\left\{1\right\}$
d. ĐKXĐ: $x\neq \frac{-1}{3}; -3$
PT $\Leftrightarrow \frac{(3x-1)(x+3)+(x-3)(3x+1)}{(3x+1)(x+3)}=2$
$\Leftrightarrow \frac{6x^2-6}{3x^2+10x+3}=2$
$\Leftrightarrow 6x^2-6=2(3x^2+10x+3)$
$\Leftrightarrow 20x+12=0$
$\Leftrightarrow x=\frac{-3}{5}$ (tm)
Vậy tập nghiệm của pt là $S=\left\{\frac{-3}{5}\right\}$
Bài 2:
a.
\(\left\{\begin{matrix} 2x-3y=11\\ 5x-4y=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 10x-15y=55\\ 10x-8y=6\end{matrix}\right.\)
\(\Rightarrow (10x-8y)-(10x-15y)=6-55\)
\(\Leftrightarrow 7y=-49\Leftrightarrow y=-7\)
\(x=\frac{3y+11}{2}=\frac{3.(-7)+11}{2}=-5\)
Vậy hpt có nghiệm $(x,y)=(-5,-7)$
b. Không đủ cơ sở để tìm $x,y$
c.
\(\left\{\begin{matrix} 5x+3y=\lambda\\ -x+\lambda y=-8\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 5x+3y=\lambda\\ -5x+5\lambda y=-40\end{matrix}\right.\)
\(\Rightarrow (3+5\lambda)y=\lambda-40\)
Nếu $\lambda = \frac{-3}{5}$ thì $0.y=\frac{-203}{5}$ (vô lý) nên hpt vô nghiệm
Nếu $\lambda \neq \frac{-3}{5}$ thì:
$y=\frac{\lambda - 40}{3+5\lambda}$
$x=8+\lambda y=\frac{\lambda ^2+24}{5\lambda +3}$
mọi người ơi giúp em mấy bài này với

Giúp mình mấy câu này với mọi người ơi. mình cảm ơn


Mấy bài này làm kiểu gì vậy ạ? Giúp với mọi người ơi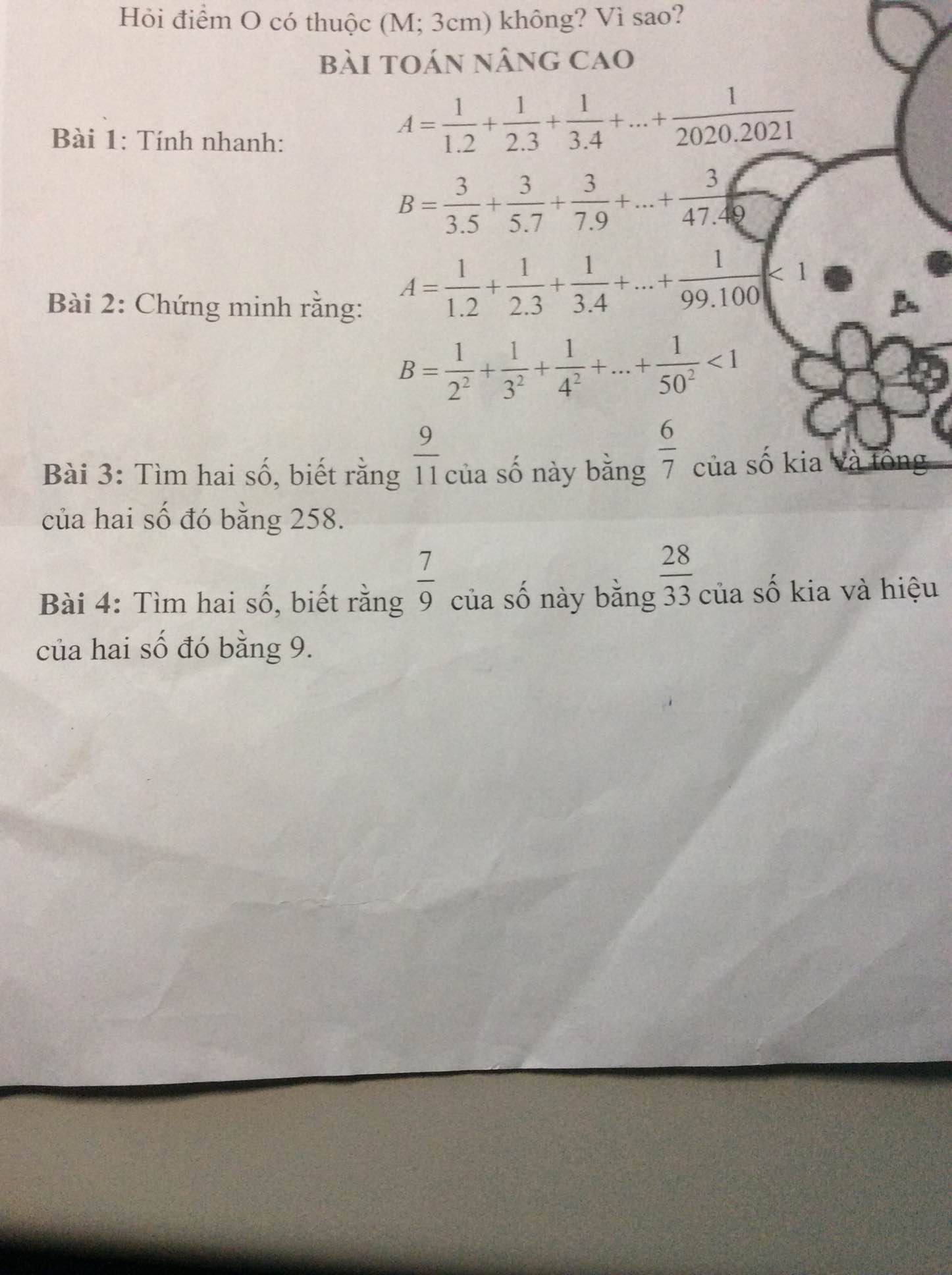
Bài 1:
a) Ta có: \(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{2020\cdot2021}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2020}-\dfrac{1}{2021}\)
\(=1-\dfrac{1}{2021}\)
\(=\dfrac{2020}{2021}\)
b) Ta có: \(B=\dfrac{3}{3\cdot5}+\dfrac{3}{5\cdot7}+...+\dfrac{3}{47\cdot49}\)
\(=\dfrac{3}{2}\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+...+\dfrac{2}{47\cdot49}\right)\)
\(=\dfrac{3}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{47}-\dfrac{1}{49}\right)\)
\(=\dfrac{3}{2}\left(\dfrac{1}{3}-\dfrac{1}{49}\right)\)
\(=\dfrac{3}{2}\cdot\dfrac{46}{147}\)
\(=\dfrac{46}{2}\cdot\dfrac{3}{147}\)
\(=\dfrac{23}{49}\)
Bài 2:
Ta có: \(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}\)
\(=\dfrac{99}{100}< 1\)