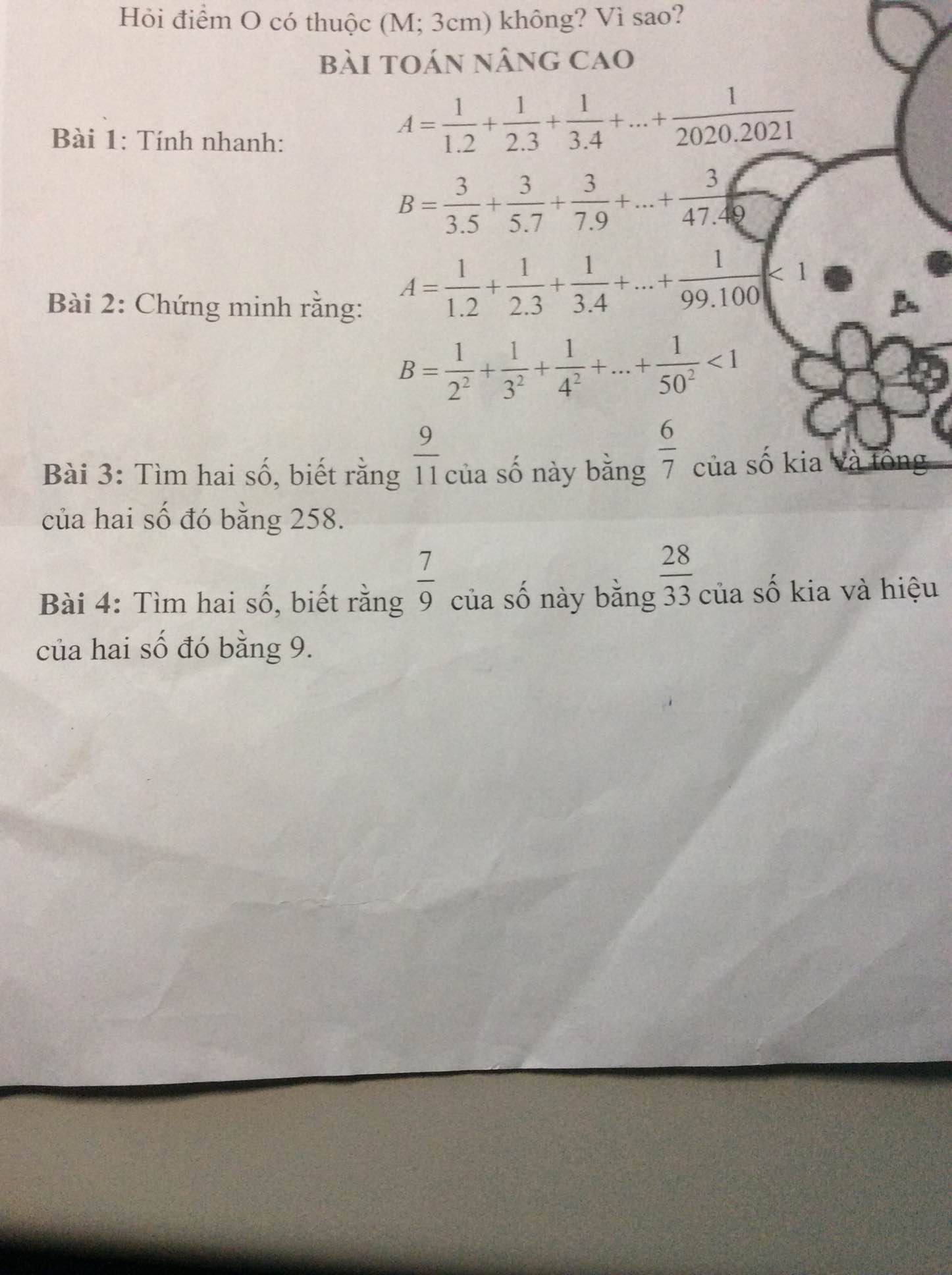Bài 1:
a) Ta có: \(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{2020\cdot2021}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2020}-\dfrac{1}{2021}\)
\(=1-\dfrac{1}{2021}\)
\(=\dfrac{2020}{2021}\)
b) Ta có: \(B=\dfrac{3}{3\cdot5}+\dfrac{3}{5\cdot7}+...+\dfrac{3}{47\cdot49}\)
\(=\dfrac{3}{2}\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+...+\dfrac{2}{47\cdot49}\right)\)
\(=\dfrac{3}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{47}-\dfrac{1}{49}\right)\)
\(=\dfrac{3}{2}\left(\dfrac{1}{3}-\dfrac{1}{49}\right)\)
\(=\dfrac{3}{2}\cdot\dfrac{46}{147}\)
\(=\dfrac{46}{2}\cdot\dfrac{3}{147}\)
\(=\dfrac{23}{49}\)
Bài 2:
Ta có: \(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}\)
\(=\dfrac{99}{100}< 1\)