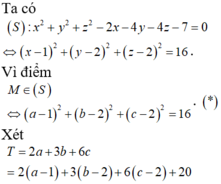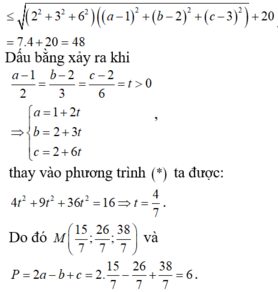Đơn giản biểu thức (2a-b)-(2a+c)+c+b
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
LT
Những câu hỏi liên quan
1) Đơn giản biểu thức
a) 4a(b-c+2a)
b)-(m-n)-(2m+n-p)
c)-(x-y)+(-3x-2y+z)
d)-(2a-2b)+(2a-3b+c)
\(a)4a\left(b-c+2a\right)\)
\(=4ab-4ac+8a^2\)
\(b)-\left(m-n\right)-\left(2m+n-p\right)\)
\(=-m+n-2m-n+p\)
\(=\left(-m-2m\right)+\left(n-n\right)+p\)
\(=p-3m\)
\(c)-\left(x-y\right)+\left(-3x-2y+z\right)\)
\(=-x+y-3x-2y+z\)
\(=\left(-x-3x\right)+\left(y-2y\right)+z\)
\(=z-4x-y\)
\(d)-\left(2a-2b\right)+\left(2a-3b+c\right)\)
\(=-2a+2b+2a-3b+c\)
\(=\left(-2a+2a\right)+\left(2b-3b\right)+c\)
\(=c-b\)
Bài 3:Đơn giản biểu thức sau khi bỏ ngoặc:
a)(-a+b)-(-a+c)
b)-(2a+b)-(2b-a+c)
Đơn giản biểu thức:
a,-(a + b - c) - (a - b + c) + 2a + 2c
b,- (3a +2b+4c) - 3(3a + 2b - 5c) + 10a - 8b - c
làm đơn giản biểu thức: cos^2A +tg^2A*cos^2A
\(=cos^2a+\dfrac{sin^2a}{cos^2a}\cdot cos^2a=cos^2a+sin^2a=1\)
Đúng 0
Bình luận (0)
Đơn giản các biểu thức sau :
a) A = ( a - b + c ) - ( b - c - d ) + ( c - d + d )
b) B = ( a + b - c ) + ( b + c - a ) - ( a - c )
c) C = - ( 4a + 5b - c ) - ( 5b + 3c )
d) D = ( a - 3b + c ) - ( 2a - b + c )
a) A = ( a - b + c ) - ( b - c - d ) + ( c - d + d )
A = a - b + c - b + c + d + c - d + d
A = a - ( b + b ) + ( c + c + c ) + ( d - d + d )
A = a - 2b + 3c + d
b) B = ( a + b - c ) + ( b + c - a ) - ( a - c )
B = a + b - c + b + c - a - a + c
B = ( a - a - a ) + ( b + b ) - ( c - c - c )
B = -a + 2b + c
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho a, b, x là những số dương. Đơn giản các biểu thức sau:
A
2
a
+
ab
1
2
3...
Đọc tiếp
Cho a, b, x là những số dương. Đơn giản các biểu thức sau: A = 2 a + ab 1 2 3 a - 1 a 3 2 - b 3 2 a - ab 1 2 - a - b a + b
Do a, b, x là những số dương nên ta có:
A = 3 b
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, gọi điểm M(a;b;c) ( với a,b,c tối giản) thuộc mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
4
z
-
7
0
sao cho biểu thức T2a+3b+6c đạt giá trị lớn nhất. Khi đó giá trị biểu thức P2a-b+c bằ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, gọi điểm M(a;b;c) ( với a,b,c tối giản) thuộc mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 4 y - 4 z - 7 = 0 sao cho biểu thức T=2a+3b+6c đạt giá trị lớn nhất. Khi đó giá trị biểu thức P=2a-b+c bằng
A. 12 7
B. 8
C. 6
D. 51 7
Cho biểu thức A = \(\frac{a^3+2a^2-1}{a^3+2a^2+2a+1}\)
a) Rút gọn biểu thức.
b) C/m nếu a nguyên thì biểu thức A là tối giản.
GIÚP MÌNH ĐI NHAAAA THANK YOU VERY MUCHHHHH!!!!!!!!!!!!!!!
Viết Năm Phân số thành một phân số
1/2; 1/5; 1/7; 1/4
bạn nào giải được không ạ ???
bạn nào biết gải giúp mình với
Đúng 0
Bình luận (0)
cho biểu thức A= \(\frac{a^3+2a^2-1}{a^3+2a^2+2a+1}\)
a, Rút gọn biểu thức
b, C\m rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a,là 1 phân số tối giản
Giải \(A=\frac{a^3+2a^2-1}{a^3+2a^22a+1}\) \(A=\frac{\left(a^3+a^2\right)+\left(a^2-1\right)}{\left(a^3+a^2\right)+\left(a^2+a\right)+\left(a+1\right)}\) \(A=\frac{a^2\left(a+1\right)\left(a+1\right)\left(a+1\right)}{a^2\left(a+1\right)+a\left(a+1\right)+\left(a+1\right)}\) \(A=\frac{\left(a+1\right)\left(a^2+a-1\right)}{\left(a+1\right)\left(a^2 +a+1\right)}\) \(A=\frac{a^2+a-1}{a^2+a+1}\) b, Gọi d là ƯCLN \(\left(a^2+a-1;a^2+a+1\right)\) \(\Rightarrow\)\(a^2+a-1⋮d\) \(a^2+a+1⋮d\) \(\Rightarrow\left(a^2+a+1\right)-\left(a^2+a-1\right)⋮d\) \(\Rightarrow2⋮d\) \(\Rightarrow d=1\) hoặc d=2 Nhận xét : \(a^2+a-1=a\left(a+1\right)-1\) Với số nguyên a ta có :a(a+1) là tích 2 số nguyên liên tiếp \(\Rightarrow a\left(a+1\right)⋮2\) \(\Rightarrow a\left(a+1\right)-1\) lẻ \(\Rightarrow a^2+a-1\) lẻ \(\Rightarrow\) d không thể bằng 2 Vậy d=1 (đpcm)
Đúng 0
Bình luận (0)