Bài 1:

a. $2^{29}< 5^{29}< 5^{39}$

$\Rightarrow A< B$

b.

$B=(3^1+3^2)+(3^3+3^4)+(3^5+3^6)+...+(3^{2009}+3^{2010})$

$=3(1+3)+3^3(1+3)+3^5(1+3)+...+3^{2009}(1+3)$

$=(1+3)(3+3^3+3^5+...+3^{2009})$

$=4(3+3^3+3^5+...+3^{2009})\vdots 4$

Mặt khác:

$B=(3+3^2+3^3)+(3^4+3^5+3^6)+....+(3^{2008}+3^{2009}+3^{2010})$

$=3(1+3+3^2)+3^4(1+3+3^2)+...+3^{2008}(1+3+3^2)$

$=(1+3+3^2)(3+3^4+....+3^{2008})=13(3+3^4+...+3^{2008})\vdots 13$

Bài 1:
c.

$A=1-3+3^2-3^3+3^4-...+3^{98}-3^{99}+3^{100}$

$3A=3-3^2+3^3-3^4+3^5-...+3^{99}-3^{100}+3^{101}$

$\Rightarrow A+3A=3^{101}+1$
$\Rightarrow 4A=3^{101}+1$

$\Rightarrow A=\frac{3^{101}+1}{4}$

Bài 2:

a. $7\vdots n+1$

$\Rightarrow n+1\in \left\{1; -1; 7; -7\right\}$

$\Rightarrow n\in \left\{0; -2; 6; -8\right\}$

b.

$2n+5\vdots n+1$
$\Rightarrow 2(n+1)+3\vdots n+1$

$\Rightarrow 3\vdots n+1$

$\Rightarrow n+1\in \left\{1; -1; 3; -3\right\}$

$\Rightarrow n\in \left\{0; -2; 2; -4\right\}$

1.

\(5=3xy+x+y\ge3xy+2\sqrt{xy}\)

\(\Leftrightarrow\left(\sqrt{xy}-1\right)\left(3\sqrt{xy}+5\right)\le0\Rightarrow xy\le1\)

\(P=\dfrac{\left(x+1\right)\left(x^2+1\right)+\left(y+1\right)\left(y^2+1\right)}{\left(x^2+1\right)\left(y^2+1\right)}-\sqrt{9-5xy}\)

\(P=\dfrac{\left(x+y\right)^3-3xy\left(x+y\right)+\left(x+y\right)^2-2xy+x+y+2}{x^2y^2+\left(x+y\right)^2-2xy+1}-\sqrt{9-5xy}\)

Đặt \(xy=a\Rightarrow0< a\le1\)

\(P=\dfrac{\left(5-3a\right)^3-3a\left(5-3a\right)+\left(5-3a\right)^2-2a+5-3a+2}{a^2+\left(5-3a\right)^2-2a+1}-\sqrt{9-5a}\)

\(P=\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{2}.2\sqrt{9-5a}\)

\(P\ge\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{4}\left(4+9-5a\right)\)

\(P\ge\dfrac{-29a^3+161a^2-277a+145}{4\left(5a^2-16a+13\right)}=\dfrac{\left(1-a\right)\left(29a^2-132a+145\right)}{4\left(5a^2-16a+13\right)}\)

\(P\ge\dfrac{\left(1-a\right)\left[29a^2+132\left(1-a\right)+13\right]}{4\left(5a^2-16a+13\right)}\ge0\)

\(P_{min}=0\) khi \(a=1\) hay \(x=y=1\)

Hai phân thức của P rất khó làm gọn bằng AM-GM hoặc Cauchy-Schwarz (nó hơi chặt)

2.

Đặt \(A=9^n+62\)

Do \(9^n⋮3\) với mọi \(n\in Z^+\) và 62 ko chia hết cho 3 nên \(A⋮̸3\)

Mặt khác tích của k số lẻ liên tiếp sẽ luôn chia hết cho 3 nếu \(k\ge3\)

\(\Rightarrow\) Bài toán thỏa mãn khi và chỉ khi \(k=2\)

Do tích của 2 số lẻ liên tiếp đều không chia hết cho 3, gọi 2 số đó lần lượt là \(6m-1\)  và \(6m+1\)

\(\Leftrightarrow\left(6m-1\right)\left(6m+1\right)=9^n+62\)

\(\Leftrightarrow36m^2=9^n+63\)

\(\Leftrightarrow4m^2=9^{n-1}+7\)

\(\Leftrightarrow\left(2m\right)^2-\left(3^{n-1}\right)^2=7\)

\(\Leftrightarrow\left(2m-3^{n-1}\right)\left(2m+3^{n-1}\right)=7\)

Pt ước số cơ bản, bạn tự giải tiếp

Đặt n² = x \(\left(x\in N\right)\)

Ta có: (x - 4)(x - 14) (x- 24) (x - 34 ) < 0

Lập bảng xét dấu (Hoặc dùng phương pháp khoảng) ta sẽ thu được kết quả:

4 < x < 14 hoặc 24 < x < 34

Dễ thấy chọn được 2 số chính phương trong các khoảng trên: x = 9; x = 25 => n = +/- 3; n = +/- 5

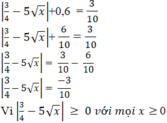
=>  không có giá trị nào của x thỏa mãn yêu cầu bài toán

Đáp án cần chọn là D

\(a,A=3+3^2+3^3+3^4+...+3^{100}\\ 3A=3^2+3^3+3^4+3^5+3^{101}\\ 3A-A=2A=3^{101}-3\\ \Rightarrow2A+3=3^{101}=3^{4.25+1}\\ \Rightarrow n=25\)

3³ⁿ⁺¹ = 9ⁿ⁺²

3³ⁿ⁺¹ = 3²⁽ⁿ⁺²⁾

3³ⁿ⁺¹ = 3²ⁿ⁺⁴

3n + 1 = 2n + 4

2n - 3n = 1 - 4

-n = -3

n = 3 

\(3^{3n+1}=9^{n+2}=\left(3^2\right)^{2n+2}=2^{4n+4}=>3n+1=4n+4=>n=-3\)

ta có : 9ⁿ⁺²=(3²)ⁿ⁺²=3²⁽ⁿ⁺²⁾=3²ⁿ⁺⁴

3³ⁿ⁺¹=9ⁿ⁺²

=>3³ⁿ⁺¹=3²ⁿ⁺⁴

=>3n+1=2n+4

=>3n-2n=4-1

=>n=3

vậy n=3

 \(3^{3n+1}=9^{n+2}\Rightarrow3^{3n+1}=\left(3^2\right)^{n+2}\)

\(\Rightarrow3^{3n+1}=3^{2\left(n+2\right)}\Rightarrow3n+1=2\left(n+2\right)\)

\(\Rightarrow3n+1=2n+4\Rightarrow3n-2n=4-1\)

\(\Rightarrow n=3\)