cho mặt cầu (S): x^2 + y^2 + z^2 -2x -2y -2z =0 và điểm A(2;2;2). Điểm B thay đổi trên mặt cầu. Diện tích của tam giác OAB có giá trị lớn nhất là?
A. 1 (đvdt)
B. 2 (đvdt)
C. căn bặc hai của 3 (đvdt)
D, 3 (đvdt)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): \(x^2+y^2+z^2-2x+6y-8z-10=0\) và mặt phẳng (P): \(x+2y-2z=0\). Viết phương trình mặt phẳng (Q) song song với (P) và tiếp xúc với (S).
Trong không gian với hệ tọa độ Oxyz cho 2 điểm A(1;0;1) và B(-1;1;0), mặt phẳng (P):\(x+y-2z-5=0\) và mặt cầu \(\left(S\right):x^2+y^2+z^2-2x+2y-6=0\).
Viết phương trình mặt phẳng (Q), biết (Q) vuông góc với (P), song song với đường thẳng AB và tiếp xúc với mặt cầu (S)
Mặt phẳng (P) có vec tơ pháp tuyến \(\overrightarrow{n}=\left(1;1;-2\right);\overrightarrow{AB}=\left(-2;1;-1\right)\)
Ta có \(\left[\overrightarrow{n};\overrightarrow{AB}\right]=\left(1;5;3\right)\)
(Q) vuông góc với (P), song song với đường thẳng AB suy ra (Q) có vectơ pháp tuyến là \(\left[\overrightarrow{n_1};\overrightarrow{AB}\right]=\left(1;5;3\right)\) nên phương trình mặt phẳng (Q) có dạng \(x+5y+3z+m=0\)
Mặt cầu (S) có tâm \(I\left(1;-1;1\right)\), bán kính R = 3
Mặt phẳng (Q) tiếp xúc với (S) có \(d\left(I,\left(Q\right)\right)=R\Leftrightarrow\frac{\left|1-5+3+m\right|}{\sqrt{35}}\)
\(\Leftrightarrow\left|m-1\right|=3\sqrt{35}\Leftrightarrow\begin{cases}m=1+3\sqrt{35}\\m=1-3\sqrt{35}\end{cases}\)
- Với \(m=1+3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1+3\sqrt{35}=0\)
- Với \(m=1-3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1-3\sqrt{35}=0\)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 2 y - 2 z - 1 = 0 và mặt phẳng ( P ) : x + y + 2 z + 2 = 0 . Giả sử điểm M thuộc (P) và điểm N thuộc (S) sao cho M N → cùng phương với vectơ a → = ( 2 ; - 1 ; 1 ) . Độ dài nhỏ nhất của đoạn MN là:
A. 2 6 +4.
B. 2 6 +2.
C. 2 6 -4.
D. 6 +2.
Cho mặt cầu ( S ) : ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 và mặt phẳng ( α ): 2x+y-2z+m=0. Các giá trị của m để ( α ) và (S) không có điểm chung là:
A. m ≤ - 9 hoặc m ≥ 21
B. m < - 9 hoặc m > 21
C. - 9 ≤ m ≤ 21
D. - 9 < m < 21
Cho mặt phẳng P : 2 x + 2 y - 2 z + 15 = 0 và mặt cầu S : x 2 + y 2 + z 2 - 2 y - 2 z - 2 = 0 . Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu (S) là:
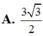
![]()
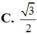
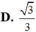
Đáp án A.
Mặt cầu (S) có tâm I(0;1;1) và bán kính R = 3
Gọi H là hình chiếu của I trên (P) và A là giao điểm của IH với (S)
Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặtcầu (S) là đoạn AH
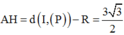
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 + 4 x - 6 y + m = 0 và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P): 2 x - 2 y - z + 1 = 0 , (Q): x + 2 y - 2 z - 4 = 0 . Tìm m để (S) cắt (d) tại 2 điểm M, N sao cho độ dài MN = 8.
A. m = 2
B. m = -12
C. m = 12
D. m = -2
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 + 4 x - 6 y + m = 0 và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P): 2 x - 2 y - z + 1 = 0 , (Q): x + 2 y - 2 z - 4 = 0 . Tìm m để (S) cắt (d) tại 2 điểm M, N sao cho độ dài MN = 8.
A. m = 2
B. m = -12
C. m = 12
D. m = -2
Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 9 và mặt phẳng (P): 2x-2y+z+14=0. Gọi M ( a ; b ; c ) là điểm thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) lớn nhất. Tính T = a + b + c .
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 2 ) 2 = 9 và mặt phẳng (P): 2x - 2y + z + 3 = 0. Gọi M(a;b;c) là điểm trên mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Khi đó:
A. a + b + c = 8.
B. a + b + c = 5.
C. a + b + c = 6.
D. a + b + c = 7.