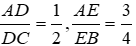Cho tam giác ABC với A=120o, AB=4cm và ac=6cm. Cho M nằm giữa BC. Tính cạnh AM
TT
Những câu hỏi liên quan
. Cho tam giác ABC, MN // BC với M nằm giữa A, B và N nằm giữa AC. Biết AN = 2cm, AB = 3AN. AC = 4CM. Tính AM
Ta có : AB=3AN
mà AN =2
=>AB= 3.2=6
=>AB=6
Ta còn có : AM = 1/2 AB
Vì M là trung điểm AB
=> AM=1/2.6
=>AM=3
Bạn kia sai rồi. Đề có cho M là trung điểm của AB đâu, chỉ cho M nằm giữa A và B thôi.
Vũ Minh Tuấn ơi ; ở giữa là ở chính giữa chứ bạn. Còn nếu ko ở chính giữa thì đề cho là ở trên cạnh chứ. Mong bạn xem sét kĩ lại
Xem thêm câu trả lời
cho tam giác abc có mn//bc (m nằm giữa a và b ;n nằm giữa a và c) .biết an=2cm;ab=3cm ;am=1cm.độ dài đoạn thẳng ac là:
a.6cm b.4cm c.8cm d.1,5cm
giúp hộ mình với
Cho tam giác ABC có BC = 12cm, AB = 6cm, AC = 9cm. Trên cạnh AB, AC lấy hai điểm M và N sao cho AM = 4cm, AN = 6cm
a) Chứng minh MN // BC
b) Tính MN
a, xét tam giác AMN và tam giác ABC có:
\(\frac{AM}{AB}=\frac{4}{6}=\frac{2}{3}\)
\(\frac{AN}{NC}=\frac{6}{9}=\frac{2}{3}\)
=> MN // BC( hệ quả định lí ta -let)
b,vì MN// BC=> \(\frac{AM}{MB}=\frac{MN}{BC}\)hay \(\frac{4}{6}=\frac{MN}{12}\Rightarrow MN=4.12:6=8cm\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB 6cm, AC 9cm. Trên cạnh AB lấy điểm M sao cho AM 4cm. Kẻ MN song song với BC (NAC). Tính AN?
Đọc tiếp
Cho tam giác ABC có AB = 6cm, AC = 9cm. Trên cạnh AB lấy điểm M sao cho AM = 4cm. Kẻ MN song song với BC (N![]() AC). Tính AN?
AC). Tính AN?
Xét ΔABC có MN//BC
nên AM/AB=AN/AC
=>AN/9=4/6=2/3
=>AN=6cm
Đúng 0
Bình luận (0)
Bài 19: Cho tam giác ABC có chu vi 18cm, các đường phân giác BD và CE. Tính các cạnh của tam giác ABC, biết A. AC 4cm, BC 8cm, AB 6cmB. AB 4cm, BC 6cm, AC 8cmC. AB 4cm, BC 8cm, AC 6cmD. AB 8cm, BC 4cm, AC 6cm
Đọc tiếp
Bài 19: Cho tam giác ABC có chu vi 18cm, các đường phân giác BD và CE. Tính các cạnh của tam giác ABC, biết
A. AC = 4cm, BC = 8cm, AB = 6cm
B. AB = 4cm, BC = 6cm, AC = 8cm
C. AB = 4cm, BC = 8cm, AC = 6cm
D. AB = 8cm, BC = 4cm, AC = 6cm
TK
Vậy AB = 4cm, BC = 8cm, AC = 6cm
Đáp án cần chọn là: C
Đúng 5
Bình luận (0)
Cho tam giác ABC có AB=4cm, AC=6cm, BC=9cm.Điểm D nằm trên cạnh BC sao cho CD=4cm. Tính AD
Cho Tam giác ABC có AB = 4cm, AC = 6cm. Trên cạnh AB và AC lần lượt lấy điểm M và N sao cho AM =1cm, AN = 1,5cm. a) Chứng minh MN // BC b) Biết MP // AC, chứng minh Tam giác AMN đồng dạng với Tam giác MBP. c) Tìm tỉ số diện tích của Tam giác AMP và Tam giác ACP. MÌNH CHỦ YẾU CẦN CÂU C NHA
a) Ta có: \(\dfrac{AM}{AB}=\dfrac{1}{4}\)
\(\dfrac{AN}{AC}=\dfrac{1.5}{6}=\dfrac{1}{4}\)
Do đó: \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)\(\left(=\dfrac{1}{4}\right)\)
Xét ΔABC có
M\(\in\)AB(gt)
N\(\in\)AC(gt)
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)(cmt)
Do đó: MN//BC(Định lí Ta lét đảo)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=6cm , AC=10cm và M là trung điểm cạnh BC sao cho AM=4cm . Chứng minh rằng : MAB=90độ
Cho tam giác ABC vuông tại A có AB=4,5cm, AC=6cm , trung tuyến AM. Đường thẳng vuông góc với AC tại C cắt tia AM tại N . a) Tính độ dài cạnh BC b) Chứng minh AN=2AM c) Phân giác của góc BAC cắt BC tại D . Chứng minh D nằm giữa B và M.
Các bạn chỉ cần làm câu c thôi nhé
a: Ta có: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=4,5^2+6^2=56,25\)
=>\(BC=\sqrt{56,25}=7,5\left(cm\right)\)
b: CN\(\perp\)CA
AB\(\perp\)CA
Do đó: CN//AB
Xét ΔMCN và ΔMBA có
\(\widehat{MCN}=\widehat{MBA}\)(hai góc so le trong, CN//AB)
CM=BM
\(\widehat{CMN}=\widehat{BMA}\)(hai góc đối đỉnh)
Do đó: ΔMCN=ΔMBA
=>MN=MA
=>M là trung điểm của AN
=>AN=2AM
c: Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{4,5}=\dfrac{CD}{6}\)
mà BD+CD=BC=7,5
nên \(\dfrac{BD}{4,5}=\dfrac{CD}{6}=\dfrac{BD+CD}{4,5+6}=\dfrac{7.5}{10.5}=\dfrac{5}{7}\)
=>\(BD=5\cdot\dfrac{4.5}{7}=\dfrac{22.5}{7}=\dfrac{45}{14}\left(cm\right)\)
Vì ΔABC vuông tại A có AM là đường trung tuyến
nên \(BM=CM=\dfrac{BC}{2}=3,75\left(cm\right)\)
Vì \(BD=\dfrac{45}{14}< \dfrac{52.5}{14}=BM\)
nên D nằm giữa B và M
Đúng 0
Bình luận (0)