Đồ thị hàm số: y = f(x) = - 3x
chứng tỏ rằng f( x1 + 4x2 ) = f(x1) +4f(x2)
Cho hàm số
y=f(x)= -5x
CMR : với x1<x2 thì f(x1)>f(x2)
f(x1+4x2)=f(x1)+4f(x2)
-f(x)=f(-x)
a) Ta có: f(x1)=-5x1; f(x2)=-5x2
Nếu x1<x2 => -5x1>-5x2 => f(x1)>f(x2) => Đpcm
b) f(x1+4x2)=-5(x1+4x2)=-5x1+4.(-5x2)=f(x1)+4. f(x2)=> Đpcm
c) -f(x)=-(-5x)=-5.(-x)=f(-x) => Đpcm
Cho hàm số y=f(x)=-5x
Chứng minh:
a) Hàm số là hàm số nghịch biến
b) f(x1+4x2)=f(x1)+4f(x2)
c) -f(x)=f(-x)
Cái này nhớ không nhầm là toán 7 :>
a) Gọi x1 và x2 là hai gtrị tương ứng của x
Giả sử x1<x2
Vì y=f(x) =-5x
\(\Rightarrow\)f(x1)=-5x1
\(\Rightarrow\)f(x2)=-5x2
mà x1<x2 \(\Rightarrow\)f(x1)>f(x2)
\(\Rightarrow\)Hs là hs nghịch biến
b) Vì y=f(x)=-5x
\(\Rightarrow\)f(x1)+4f(x2)
=-5x1+4(-5)x2
=-5(x1+4x2) (*)
\(\Rightarrow\)f(x1+4x2)=-5(x1+4x2) (**)
Từ (*), (**) \(\Rightarrow\)f(x1+4x2)=f(x1)+4f(x2)
c) Vì y=f(x)=-5x
\(\Rightarrow\)-f(x)=5x (*)
\(\Rightarrow\)f(-x)=-5(-x) =5x (**)
Từ (*) và (**) \(\Rightarrow\)-f(x) =f(-x)
Cho hàm số y = f ( x ) có đồ thị f ( x ) như hình bên. Biết rằng: f ( x 3 ) = f ( x o ) và f ( x 1 ) + f ( x 2 ) = f ( x 5 ) + f ( x 7 ) Giá trị lớn nhất của hàm số y = f ( x ) trên [ x 1 ; x 7 ] bằng
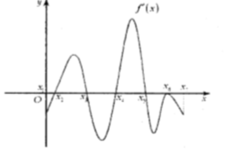
A . f ( x 1 )
B . f ( x 3 )
C . f ( x 5 )
D . f ( x 7 )
cho hàm số y=-2x+1a)Xác định tọa độ giao điểm của đồ thị hàm số trên và Ox,Oy
b)CMR:f(x1)+f(x2)=f(x1+x2)+1
c)Tìm tọa độ giao điểm của đồ thị hàm số trên và đồ thị hàm số y=|x|
a) Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Ox là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=-2x+1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+1=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x=-1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Oy là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Bài 1: Cho hàm số Y= f(x)=k.x ( k là hằng số , k khác 0). Chứng minh rằng:
a, f(10x) =10.f(x)
b, f(x1 + x2 ) = f(x1) + f(x2)
Bài 2: cho các hàm số y=2x và y= \(\frac{18}{x}\)không vẽ đồ thị . Tìm tọa độ giao điểm của hàm số đã cho.
Bài 1: Cho hàm số Y= f(x)=k.x ( k là hằng số , k khác 0). Chứng minh rằng:
Giải thích các bước:
a)f(10x) = 10f(x)
ta có:
y= f (x) =kx
=>f(10x) = k(10x) =10kx (*)
=>10f(x) = 10kx (**)
Từ (*) và (**)
=> f(10x) =10f(x)
=>đpcm
b)
f(x1 - x2) = k.(x1 - x2) (1)
f(x1) - f(x2) = k.x1 - k.x2 = k.(x1 - x2) (2)
Từ (1) và (2) => đpcm
Giải thích các bước:
a)f(10x) = 10f(x)
ta có:
y= f (x) =kx
=>f(10x) = k(10x) =10kx (*)
=>10f(x) = 10kx (**)
Từ (*) và (**)
=> f(10x) =10f(x)
=>đpcm
b)
f(x1 - x2) = k.(x1 - x2) (1)
f(x1) - f(x2) = k.x1 - k.x2 = k.(x1 - x2) (2)
Từ (1) và (2) => đpcm
Cho hàm số bậc 4 y = f(x) có đồ thị như hình vẽ bên. Biết hàm số y = f(x) đạt cực trị tại các điểm x1,x2,x3 thỏa mãn x3 = x1+2, f(x1) + f(x3) +\(\dfrac{2}{3}\)f(x2) = 0 và (C) nhận đường thẳng x = x2 làm trục đối xứng. Gọi S1,S2,S3,S4 là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số \(\dfrac{S_1+S_2}{S_3+S_4}\) gần với kết quả nào nhất :
Có thể nghịch suy để chọn hàm làm trắc nghiệm
Do \(x_2=\dfrac{x_3-x_1}{2}=1\) nên hàm có dạng: \(y=a\left(x-1\right)^4-b\left(x-1\right)^2+c\) với a;b;c dương
\(y'=0\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=\dfrac{b}{2a}\end{matrix}\right.\) \(\Rightarrow x_1;x_3\) thỏa mãn \(\left(x-1\right)^2=\dfrac{b}{2a}\) và \(f\left(x_2\right)=c\)
\(f\left(x_1\right)+f\left(x_3\right)+\dfrac{2}{3}f\left(x_2\right)=0\Leftrightarrow2f\left(x_1\right)+\dfrac{2}{3}f\left(x_2\right)=0\)
\(\Leftrightarrow a.\left(\dfrac{b}{2a}\right)^2-b\left(\dfrac{b}{2a}\right)+c+\dfrac{c}{3}=0\Rightarrow-\dfrac{b^2}{4a}+\dfrac{4c}{3}=0\)
Tới đây chọn \(a=3;c=1;b=4\) được hàm \(f\left(x\right)=3\left(x-1\right)^4-4\left(x-1\right)^2+1\)
Dễ dàng tính ra \(x_3=1+\sqrt{\dfrac{2}{3}}\) ; \(x_0=1+\sqrt{\dfrac{1}{3}}\) (với \(x_0\) là giao bên phải của đồ thị và trục hoành); \(f\left(x_1\right)=f\left(x_3\right)=-\dfrac{1}{3}\)
\(S_1+S_2=\int\limits^{x_0}_1f\left(x\right)dx-\int\limits^{x_3}_{x_0}f\left(x\right)dx\approx0,41\)
\(\dfrac{S_1+S_2}{S_3+S_4}=\dfrac{0,41}{\left(1+\dfrac{1}{3}\right)\left(x_3-1\right)-0,41}\approx0,6\)
Vẽ đồ thị hàm số
a) \(y=\frac{1}{2}\left(x-\left|x\right|\right)\)
b) Chứng minh rằng hàm số y=f(x)=ax có tính chất :f(x1+x2)=f(x1)+f(x2)
Cho hàm số y = f(x) = 1/2x.
chứng tỏ rằng x1 > x2 thì f(x1) > f(x2)
cảm ơn vì đã giải nha :) :)
Ta co: y = 1/2 x
khi x1 > x2 thi suy ra:
1/2.x1 > 1/2 . x2 (dpcm)
Viết công thức của hàm số y = f(x) biết rằng y tỷ lệ thuận với x theo hệ số tỷ lệ a/ Tìm x để f(x) = -5 b/ Chứng tỏ rằng nếu x1> x 2 thì f(x1) > f(x2)
Cho hàm số y=f(x)=2x-3. X lấy giá trị thực bất kì x1, x2 sao cho x1 < x2. Chứng tỏ f(x1) < f(x2). Kết luận về tính biến thiên của hàm số