(X-2)x(X+7)=0
Tìm X![]()
Ai đúng tích cho!
(1/2.x-7).(x+2)=0
tìm x
`(1/2x-7)(x+2)=0`
`<=>` \(\left[ \begin{array}{l}\dfrac12x-7=0\\x+2=0\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}\dfrac12x=7\\x=-2\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x=14\\x=-2\end{array} \right.\)
Vậy `x=14` hoặc `x=-2`
Ta có: \(\left(\dfrac{1}{2}x-7\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x-7=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=14\\x=-2\end{matrix}\right.\)
Cho hàm số f ( x ) = x 2 , x ≥ 1 2 x 3 1 + x , 0 ≤ x ≤ 1 x sin x , x < 0 Tìm khẳng định đúng trong các khẳng định sau:
A. f(x) liên tục trên R.
B. f(x) liên tục trên R \ {0}.
C. f(x) liên tục trên R \ {1}.
D. f(x) liên tục trên R \ {0; 1}.
Chọn A.
Với x >1 ta có hàm số f(x) = x2 liên tục trên khoảng (1; +∞). (1)
Với 0 < x < 1 ta có hàm số 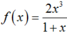 liên tục trên khoảng (0; 1). (2)
liên tục trên khoảng (0; 1). (2)
Với x < 0 ta có f(x) = x.sinx liên tục trên khoảng (-∞; 0). (3)
Với x = 1 ta có f(1) = 1; 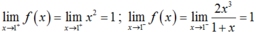
Suy ra ![]() .
.
Vậy hàm số liên tục tại x = 1.
Với x = 0 ta có f(0) = 0; 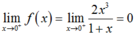 ;
;
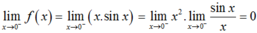 suy ra
suy ra ![]() .
.
Vậy hàm số liên tục tại x = 0. (4)
Từ (1), (2), (3) và (4) suy ra hàm số liên tục trên R.
Chọn A.
(x - 1 ) . ( x +2) . (-x - 3) = 0
Tìm các số nguyên x , thỏa mãn :
( x - 7 ) ( x + 3 ) < 0
a: (x-1)(x+2)(-x-3)=0
=>(x-1)(x+2)(x+3)=0
=>\(\left[{}\begin{matrix}x-1=0\\x+2=0\\x+3=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\\x=-2\\x=-3\end{matrix}\right.\)
b: (x-7)(x+3)<0
TH1: \(\left\{{}\begin{matrix}x-7>0\\x+3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>7\\x< -3\end{matrix}\right.\)
=>\(x\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}x-7< 0\\x+3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 7\\x>-3\end{matrix}\right.\)
=>-3<x<7
mà x nguyên
nên \(x\in\left\{-2;-1;0;1;2;3;4;5;6\right\}\)
c,(x-1)43=(x-1)2021
tìm x
ai giúp mik vs mik đang gấp
Ai nhanh micnhf tích cho nha
mik cảm ơn trước
\(\left(x-1\right)^{43}=\left(x-1\right)^{2021}\)
\(\Rightarrow\left(x-1\right)^{43}\left[\left(x-1\right)^{1978}-1\right]=0\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^{1978}=1\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\\x=0\end{matrix}\right.\)
(x-2/5).(x+2/7)>0
( 2x-1/2).(3x-1/3)<0
x+3/2 phần x-2/3 <0
Tìm x
Các bạn giúp mk nha mk cần gấp
a: Ta có: \(\left(x-\dfrac{2}{5}\right)\left(x+\dfrac{2}{7}\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{2}{5}\\x< -\dfrac{2}{7}\end{matrix}\right.\)
2x(3x-7)(6x+5)(x-3)-2019=0
Tìm x nha
Cho phương trình x2 - 2(k - 2)x - 2k - 5 = 0
Tìm k để phương trình có 2 nghiệm x1, x2 thỏa mãn 2x1 - x2 = 7
PT có 2 nghiệm \(\Leftrightarrow\Delta'=\left(k-2\right)^2-\left(-2k-5\right)\ge0\)
\(\Leftrightarrow k^2-4k+4+2k+10\ge0\\ \Leftrightarrow k^2-2k+14\ge0\\ \Leftrightarrow k\in R\)
Vậy PT luôn có 2 nghiệm
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=2\left(k-2\right)\left(1\right)\\x_1x_2=-2k-5\left(2\right)\end{matrix}\right.\)
Lại có \(2x_1-x_2=7\left(3\right)\)
\(\left(1\right)\left(3\right)\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\left(k-2\right)\\2x_1-x_2=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_1=2k+3\\x_2=2x_1-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{2k+3}{2}\\x_2=\dfrac{4k+6}{2}-7=\dfrac{4k-8}{2}=2k-4\end{matrix}\right.\)
Thay vào \(\left(2\right)\Leftrightarrow\dfrac{\left(2k+3\right)\left(2k-4\right)}{2}=-2k-5\)
\(\Leftrightarrow\left(2k+3\right)\left(k-2\right)=-2k-5\\ \Leftrightarrow2k^2-k-6+2k+5=0\\ \Leftrightarrow2k^2+k-1=0\\ \Leftrightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-1\end{matrix}\right.\)
(\(x^2\)-1)\(\sqrt[]{x}\)=-0
tìm x
giúp mình nha mình tick cho
ĐK:\(x\ge0\)
\(\left(x^2-1\right)\sqrt{x}=0\Leftrightarrow\left(x-1\right)\left(x+1\right)\sqrt{x}=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\\sqrt{x}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-1\left(ktm\right)\\x=0\left(tm\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\)
Ủa lớp 7 sao học căn r nè
cho pt x^3+(1-m).x^2-m^2=0
tìm m để pt có đúng
a. 2 nghiệm
b. 3 nghiệm
c. 3 nghiệm dương phân biệt
d. 3 nghiệm âm phân biệt
mn giải giúp mk vs, giải chi tiết cho mk dễ hiểu nhé, mk cảm ơn rất nhiều ^-^
Cho pt: X^2 - 2(m-1)x + m^2 - 2m = 0
tìm M để pt vô nghiệm
\(\Delta'=\left(m-1\right)^2-\left(m^2-2m\right)=m^2-2m+1-m^2+2m=1>0\)
vậy pt có 2 nghiệm pb
hay ko có gtri m để pt vô nghiệm
\(\Delta'=\left(m-1\right)^2-\left(m^2-2m\right)=m^2-2m+1-m^2+2m=1>0.\)
\(\Rightarrow\) Phương trình luôn có nghiệm với mọi x thuộc R.
\(\Rightarrow\) \(m\in\phi.\)