XÁC ĐỊNH CÁC ĐIỂM SAU TRÊN MẶT PHẲNG TỌA ĐỘ
A(-1;3)
B(2;3)
C(3;1/2)
D(0;-3)
E(3;0)
Trên mặt phẳng tọa độ Oxy, cho điểm A( 5; 6). Xác định vị trí tương đối của đường tròn (A; 5) với các trục tọa độ?
A. Đường tròn tiếp xúc trục Oy.
B. Đường tròn tiếp xúc với trục Ox.
C. Đường tròn không cắt trục Ox.
D. Đường tròn không cắt trục Oy.
Đáp án A
Ta có khoảng cách từ A đến trục Ox bằng 6 > R.
Đường tròn (A; R) cắt trục Ox tại 2 điểm phân biệt .
Khoảng cách từ A đến trục Oy bằng 5 = R..
Do đó, đường tròn (A; R) tiếp xúc với trục Oy.
Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 4). Hãy xác định vị trí tương đối của đường tròn (A; 3) và các trục tọa độ
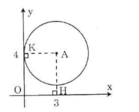
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.
Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 4). Hãy xác định vị trí tương đối của đường tròn (A; 3) và các trục tọa độ.
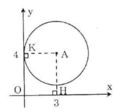
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.
Trên mặt phẳng tọa độ Oxy, cho điểm A(2; 4). Hãy xác định vị trí tương đối của đường tròn (A; 2) và các trục tọa độ.
Do A(2; 4) nên A cách trục Ox 2 đơn vị, cách trục Oy 4 đơn vị
Khi đó đường tròn (A; 2) tiếp xúc với trục Ox và không giao nhau với trục Oy
Trên mặt phẳng tọa độ Oxy, cho điểm A(3;4). Hãy xác định vị trí tương đối của đường tròn (A; 3) và các trục tọa độ.
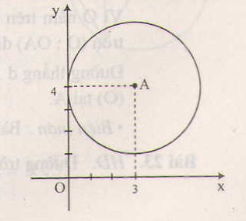
- Khoảng cách từ tâm A đến trục Ox là 4.
Vậy d>R, do đó đường tròn và trục Ox không giao nhau.
- Khoảng cách từ tâm A tới trục Oy là 3.
Vậy d=R, do đó đường tròn và trục Oy tiếp xúc nhau.
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4).
a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y = 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox.
b) Xác định các hệ số a và b biết đồ thị hàm số y= ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút).
c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ nhất).
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
Vậy: (d): y=2x+b
Vì (d) đi qua điểm C(-1;4) nên
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
hay b=6
Vậy: (d): y=2x+6
Thay y=0 vào (d), ta được:
2x+6=0
hay x=-3
Vậy: A(-3;0)
b) Vì y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\b=a+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=\dfrac{-4}{5}+4=\dfrac{-4}{5}+\dfrac{20}{5}=\dfrac{16}{5}\end{matrix}\right.\)
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4).
a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y = 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox.
b) Xác định các hệ số a và b biết đồ thị hàm số y= ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút).
c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ nhất).
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên ta có: \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
=> (d): y=2x+b
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
\(\Leftrightarrow b=6\)
Vậy: (D): y=2x+6
Thay y=0 vào (d),ta được:
\(2x+6=0\)
\(\Leftrightarrow x=-3\)
Vậy: A(-3;0)
b) Vì đồ thị hàm số y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\-a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=4+a=4+\dfrac{-4}{5}=4-\dfrac{4}{5}=\dfrac{16}{5}\end{matrix}\right.\)
Vậy: \(a=-\dfrac{4}{5}\); \(b=\dfrac{16}{5}\)
c) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(-3-4\right)^2+\left(0-0\right)^2}=7\)(cm)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(-3+1\right)^2+\left(0-4\right)^2}=2\sqrt{5}\left(cm\right)\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(4+1\right)^2+\left(0-4\right)^2}=\sqrt{41}\left(cm\right)\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC\)
\(=7+2\sqrt{5}+\sqrt{41}\)
\(\simeq17,9\left(cm\right)\)
Biểu diễn các điểm A(5;0); B(5;-3) trên mặt phẳng tọa độ và xác định điểm đối xứng vs A;B
Trên mặt phẳng tọa độ Oxy, cho điểm A(3;4). Hãy xác định vị trí tương đối của đường tròn (A;3) và các trục tọa độ.
- Khoảng cách từ tâm A đến trục Ox là 4.
Vậy d>R, do đó đường tròn và trục Ox không giao nhau.
- Khoảng cách từ tâm A tới trục Oy là 3.
Vậy d=R, do đó đường tròn và trục Oy tiếp xúc nhau.
bài 1: xác định các điểm sau trên mặt phẳng tọa độ: A(-1;3) ; B(2;3) ; C(3;\(\frac{1}{2}\))
giúp với