Bài 3,4,5
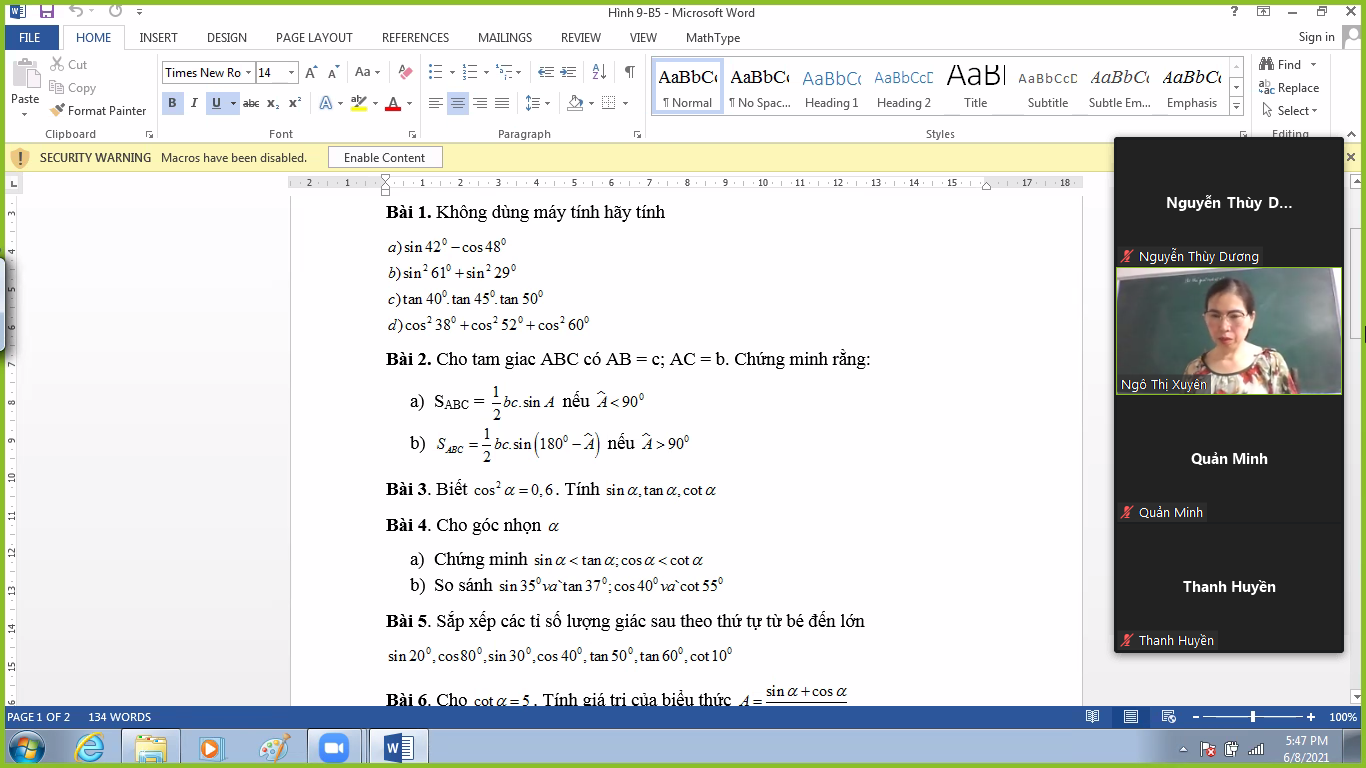
bài 3,4,5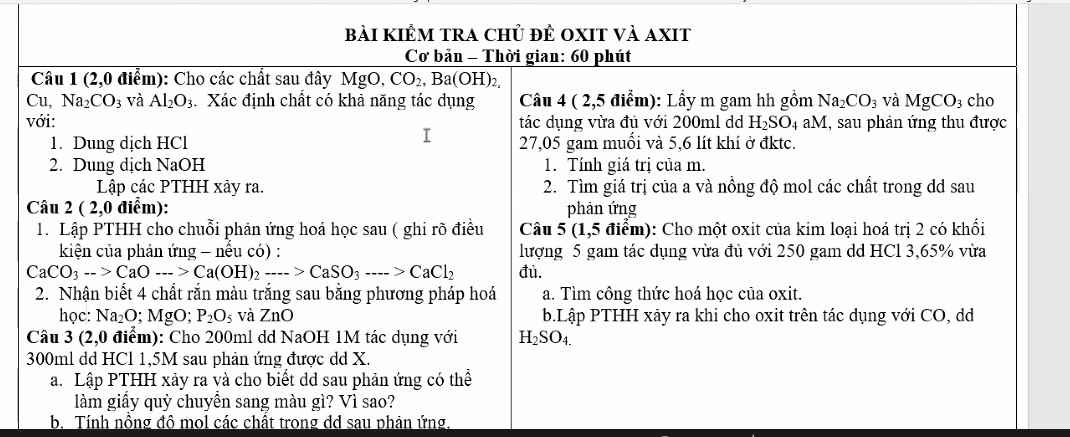
Giúp mình bài 3,4,5 nha


Giúp mình bài 3,4,5 nha
tham khảo
câu 3
- Hình ảnh thiên nhiên – cây, lá cỏ, cái hoa (vế A) được so sánh với gang tay, sợi tóc, cái cúc (vế B) – những hình ảnh nhỏ xinh gắn với thế giới con người. Tiếng hót của chim – âm thanh được so sánh với nước, mây trời giúp người đọc cảm nhận được một cách cụ thể sự trong trẻo và cao vút của tiếng chim.
→ Thiên nhiên như nhỏ lại, gần gũi và thật dễ thương trong đôi mắt trẻ thơ.
câu 4
Trong dòng thơ: “Những làn gió thơ ngây”:
Nhà thơ dùng từ “thơ ngây” – thường dùng để nói về đặc điểm của con người, đặc biệt là trẻ em – để nói về gió.
→ Biện pháp tu từ nhân hóa khiến làn gió mang vẻ đáng yêu, hôn nhiên của trẻ thơ.
câu 5
Điệp ngữ trong đoạn thơ là các từ ngữ như: “rất”, “từ cái…”, “từ…”
- Tác dụng: nhằm mục đích liệt kê những hình ảnh phong phú trong lời ru của mẹ, nhấn mạnh vẻ đẹp của những hình ảnh ấy.
Giúp em bài 3,4,5.Gấp ạ
Câu 4 số mol h2so4 dùng để trung hòa 500g là n=1.0,02.10=0,2mol
2M+2H2O->2MOH+H2
a a
M2O+H2O->2MOH
b 2b
2MOH+H2SO4-> M2SO4+2H2O
n(MOH)=2n(H2SO4)=0,2.2=0,4mol
Ta có hệ a+2b=0,4
aM+b(2M+16)=10,8
<=> (a+2b)M +16b=10,8
0,4M+16b=10,8
<=>M+40b=27
Ta có M<27 và b<0,2
=> M chỉ có thể là Na(M=23)
b=0,1 ; a=0,2
Lần sau em đăng tách ra 1-2 bài cho 1 câu hỏi nha
GIÚP EM BÀI 3,4,5 VỚI Ạ..
GIÚP EM BÀI 3,4,5 VỚI Ạ
Bài 4:
2: Xét ΔBAK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
Giúp em bài 3,4,5 với ạ
Bài 5:
\(\cos\alpha=\sqrt{1-\dfrac{1}{25}}=\dfrac{2\sqrt{6}}{5}\)
\(\tan\alpha=\dfrac{1}{5}:\dfrac{2\sqrt{6}}{5}=\dfrac{\sqrt{6}}{12}\)
\(\cot\alpha=2\sqrt{6}\)
GIÚP EM BÀI 3,4,5 VỚI Ạ

Bài 5:
\(\cos\alpha=\sqrt{1-\dfrac{1}{25}}=\dfrac{2\sqrt{6}}{5}\)
\(\tan\alpha=\dfrac{1}{5}:\dfrac{2\sqrt{6}}{5}=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{24}\)
\(\cot\alpha=1:\dfrac{\sqrt{6}}{24}=4\sqrt{6}\)
GIÚP EM BÀI 3,4,5 Ạ.GẤP Ạ..
\(5,\\ K=\sqrt{5x-9+6\sqrt{5x-9}+9}+\sqrt{5x-9-6\sqrt{5x-9}+9}\\ K=\sqrt{\left(\sqrt{5x-9}+3\right)^2}+\sqrt{\left(\sqrt{5x-9}-3\right)^2}\\ K=\sqrt{5x-9}+3+\sqrt{5x-9}-3=2\sqrt{5x-9}\ge0,\forall x\\ K_{min}=0\Leftrightarrow\sqrt{5x-9}=0\Leftrightarrow x=\dfrac{9}{5}\)
\(3,\\ 1,A=\dfrac{1,44+7}{\sqrt{1,44}}=\dfrac{7,44}{1,2}=\dfrac{31}{5}\\ 2,B=\dfrac{x-3\sqrt{x}+\left(2\sqrt{x}-1\right)\left(\sqrt{x}+3\right)-2x+\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ B=\dfrac{x-3\sqrt{x}+2x+5\sqrt{x}-3-2x+\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ B=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(3,S=\dfrac{1}{B}+A=\dfrac{\sqrt{x}+3}{\sqrt{x}}+\dfrac{x+7}{\sqrt{x}}=\dfrac{x+\sqrt{x}+10}{\sqrt{x}}\\ S=\sqrt{x}+1+\dfrac{10}{\sqrt{x}}\ge2\sqrt{\sqrt{x}\cdot\dfrac{10}{\sqrt{x}}}+1=2\sqrt{10}+1\left(BĐT.cosi\right)\)
Dấu \("="\Leftrightarrow x=10\)
\(1,HC=BC-HB=6\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=16\\AC^2=CH\cdot BC=48\\AH^2=BH\cdot HC=12\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=4\left(cm\right)\\AC=4\sqrt{3}\left(cm\right)\\AH=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
\(2,\widehat{ADB}=\widehat{AHB}\left(=90^0\right)\) nên \(ADHB\) nội tiếp
\(\Rightarrow\widehat{HDB}=\widehat{HAB}\left(cùng.chắn.HB\right)\)
Mà \(\widehat{HAB}=\widehat{ACB}\left(cùng.phụ.\widehat{HAC}\right)\)
\(\Rightarrow\widehat{HDB}=\widehat{ACB}\)
\(\left\{{}\begin{matrix}\widehat{HDB}=\widehat{ACB}\left(cm.trên\right)\\\widehat{KBC}.chung\end{matrix}\right.\Rightarrow\Delta BHD\sim\Delta BKC\left(g.g\right)\\ \Rightarrow\dfrac{BD}{BC}=\dfrac{BH}{BK}\Rightarrow BD\cdot BK=BH\cdot BC\)
\(c,\) Áp dụng công thức tính diện tích hình tam giác bằng