1. Cho tam giác ABC có 3 góc nhọn, kẻ đường cao AH. Gọi E; F là các điểm đối xứng của H qua các cạnh AB và AC. Đoạn thẳng EF cắt AB và AC tại M và N. Chứng minh MC// EH và NB//FH
DC
Những câu hỏi liên quan
cho tam giác ABC có 3 góc 3 góc nhọn, đường cao AH . Vẽ ra ngoài tam giác ABC tam giác ABE và ACF vuông cân A Từ e và f kẻ EK, FN vuông AH
a) CM EK=FN
b) gọi I là giao của EFvaf HA tìm điều kiện của tam giác ABC để EF=2 AI
a) Ta chứng minh tam giác KAE = tam giác HBA
Hai tam giác trên là hai tam giác vuông, có hai cạnh huyền bằng nhau EA = BA (giả thiết). \(\widehat{EAK}=\widehat{HBA}\) (vì đều phụ với góc \(\widehat{BAH}\), góc \(\widehat{EAK}\) phụ với \(\widehat{BAH}\)vì tổng của chúng bằng 180 độ trừ đi góc vuông \(\widehat{EAB}\), còn góc \(\widehat{HBA}\)phụ với \(\widehat{BAH}\) vì là hai góc nhọn của tam giác vuông),
Hai tam giác vuông có hai góc đôi một bằng nhau thì cặp góc còn lại cũng bằng nhau.
Vậy tam giác KAE = tam giác HBA. Suy ra EK = AH.
Chứng minh tương tự: FN = AH
=> EK = FN (=AH)
b) Do EK và FN cùng vuông góc với AH nên EK // FN, mà EK = FN nên EKFN là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
=> đường chéo EF cắt KN tại trung điểm I của EF.
Nếu tam giác AEF vuông tại A thì EF = 2 AI (với AI là đường trung tuyến) và ngược lại. Khi đó có 4 góc ở đỉnh A kề nhau mà 3 góc bằng 90 độ => Góc \(\widehat{BAC}=90^o\). Vậy Tam giác ABC là tam giác vuông.
Đúng 0
Bình luận (0)
Em có góp ý với quản lí :Nếu đã có từ " góc " thì ko cần phải thêm dấu mũ vào tên góc.
VD : " Góc \(BAH\) " chứ ko phải là " Góc \(\widehat{BAH}\) "
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB <AC) có 3 góc nhọn nội tiếp trong đường tròn (O; R). Vẽ đường
cao AH của tam giác ABC, đường kính AD của đường tròn. Gọi E, F lần lượt là chân đường vuông
góc kẻ từ C và B xuông đường thẳng AD. M là trung điểm của BC.
a) Chứng minh tứ giác BMOF nội tiếp.
b) Gọi K là giao điểm của AD và BC. Chứng minh KH.ED = KE.BH
a)
Xét (O) có
M là trung điểm của dây BC(gt)
nên OM\(\perp\)BC(Định lí đường kính vuông góc với dây)
Xét tứ giác BMOF có
\(\widehat{BFO}+\widehat{BMO}=180^0\left(90^0+90^0=180^0\right)\)
nên BMOF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 3
Bình luận (0)
Cho tam giác ABC ( AB < AC) có 3 góc nhọn nội tiếp (O). AH là đường cao của tam giác ABC. Kẻ đường kính AD của (O). Từ 2 điểm B,C kẻ BE và CF vuông góc với AD lần lượt tại E,F.
Gọi I là trung điểm của BC. Chứng minh IE = IF.
Cho tam giác ABC (AB AC) có 3 góc nhọn nội tiếp trong đường tròn (O; R). Vẽ đường cao AH của tam giác ABC, đường kính AD của đường tròn. Gọi E, F lần lượt là chân đường vuông góc kẻ từ C và B xuống đường thẳng AD. M là trung điểm của BC.Tìm khẳng định sai ? A. Tứ giác ABHF nội tiếp B. Tứ giác BMFO nội tiếp. C.
H
E
/
/
B
D
D. Có ít nhất một khẳng định sai
Đọc tiếp
Cho tam giác ABC (AB < AC) có 3 góc nhọn nội tiếp trong đường tròn (O; R). Vẽ đường cao AH của tam giác ABC, đường kính AD của đường tròn. Gọi E, F lần lượt là chân đường vuông góc kẻ từ C và B xuống đường thẳng AD. M là trung điểm của BC.
Tìm khẳng định sai ?
A. Tứ giác ABHF nội tiếp
B. Tứ giác BMFO nội tiếp.
C. H E / / B D
D. Có ít nhất một khẳng định sai
Chọn đáp án D

* Chứng minh các tứ giác ABHF và BMFO nội tiếp.
- Từ giả thiết suy ra: 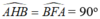
=> H và F thuộc đường tròn đường kính AB (quỹ tích cung chứa góc)
Vậy tứ giác ABHF nội tiếp đường tròn đường kính AB
- Gọi M là trung điểm của BC (gt), suy ra: OM ⊥ BC
Khi đó: 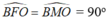
Nên M, F thuộc đường tròn đường kính OB(quỹ tích cung chứa góc).
Vậy tứ giác BMOF nội tiếp đường tròn đường kính OB
* Chứng minh HE // BD.
Dễ chứng minh tứ giác ACEH nội tiếp đường tròn đường kính AC.
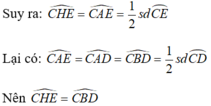
Và chúng ở vị trí so le trong suy ra: HE // BD
Đúng 0
Bình luận (0)
Bài 1 :Cho tam giác ABC nhọn, các đường cao BH,CK. Gọi D và E lần lượt là chân đường vuông góc kẻ từ B,C xuống đường thẳng HK. Chứng minh DK=EH
Bài 2 : Cho tam giác ABC vuông tại A, đường cao AH.Qua trung điểm M của cạnh AC, kẻ MN vuông góc với BC tại N. Gọi K là trung điểm AH. Chứng minh BK vuông góc với AN
Bài 1:
a: Ta có: ΔBKC vuông tại K
mà KM là đường trung tuyến
nên KM=BC/2(1)
Ta có: ΔBHC vuông tại H
mà HM là đường trung tuyến
nên HM=BC/2(2)
Từ (1)và (2) suy ra MH=MK
hay ΔMHK cân tại M
b: Kẻ MN vuông góc với HK
=>N là trung điểm của HK
Xét hình thang CBDE có
M là trung điểm của BC
MN//DB//EC
DO đó: N là trung điểm của DE
=>DK=HE
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn và AB <AC nội tiếp trong đường tròn tâm O. Kẻ đường cao AH và đường kính A A'. Gọi E và F theo thứ tự là chân đường vuông góc kẻ Từ B và C xuống đường kính A A' gọi M là trung điểm B C. Cm MD = ME =MF
Cho tam giác ABC nhọn, đường cao AH (H thuộc BC ), kẻ HI vuông góc AB tại I, trên tia đối của tia IH lấy điểm E sao cho EI bằng HI a, chứng minh AEAH Cho tam giác ABC nhọn , đường cao AH (H thuộc BC ), kẻ HI vuông góc AB tại I , trên tia đối của tia IH lấy điểm E sao cho EI bằng HI a, chứng minh AEAH b, kẻ HK vuông góc AC tại K , trên tia đối của tia KH lấy điểm F sao cho FKHK . chứng minh tam giác AEFcânc, chứng minh HA là phân giác góc MHN d, chứng minh AH,BN, CM đồng quy
Đọc tiếp
Cho tam giác ABC nhọn, đường cao AH (H thuộc BC ), kẻ HI vuông góc AB tại I, trên tia đối của tia IH lấy điểm E sao cho EI bằng HI a, chứng minh AE=AH Cho tam giác ABC nhọn , đường cao AH (H thuộc BC ), kẻ HI vuông góc AB tại I , trên tia đối của tia IH lấy điểm E sao cho EI bằng HI
a, chứng minh AE=AH
b, kẻ HK vuông góc AC tại K , trên tia đối của tia KH lấy điểm F sao cho FK=HK . chứng minh tam giác AEFcân
c, chứng minh HA là phân giác góc MHN
d, chứng minh AH,BN, CM đồng quy
a: Xét ΔAEH có
AB vừa là đường cao, vừa là trung tuyến
=>ΔAEH cân tại A
=>AE=AH
b: Xét ΔAHF có
AC vừa là đường cao, vừa là trung tuyến
=>ΔAHF cân tại A
=>AH=AF=AE
Đúng 0
Bình luận (0)
1. Cho tam giác ABC có 3 góc nhọn, kẻ đường cao AH. Gọi E; F là các điểm đối xứng của H qua các cạnh AB và AC. Đoạn thẳng EF cắt AB và AC tại M và N. Chứng minh MC// EH và NB//FH
Cho tam giác ABC có 3 góc nhọn. Gọi AH là đường cao lớn nhất trong ba đường cao. BE là trung tuyến kẻ từ đỉnh B. Cho biết AH=BE.
a) Chứng minh: góc CBE = 30 độ
b) Chứng minh: góc ABC < hoặc = 60 độ.
c) Tam giác ABC thoả mãn điều kiện gì thì góc B= 60 độ.
cho tam giác ABC có 3 góc nhọn, kẻ đường cao AH. Chứng minh sin A + cos A > 1



