1)xác định giá trị của ab,biết
a+b=10 và a2+b2=52
2) xác định giá trị x3+y3
x2+y2=20 và x+y=2
Tìm các giá trị của a,b,c để phấn thức sau được xác định a 2 + b 2 + c 2 ( a + b + c ) 2 + ( a b + b c + c a ) 2 ( a + b + c ) 2 - ( a b + b c + c a )
Cho biểu thức
Q = a a 2 - b 2 - 1 + a a 2 - b 2 : b a - a 2 - b 2 v ớ i a > b > 0
Xác định giá trị của Q khi a = 3b
Cho biểu thức
Q = a a 2 − b 2 − 1 + a a 2 − b 2 : b a − a 2 − b 2 vói a > b > 0
a) Rút gọn Q.
b) Xác định giá trị của Q khi a = 3b.
a) Rút gọn
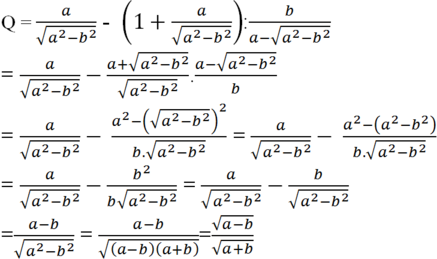
b) Thay a = 3b vào ta được:
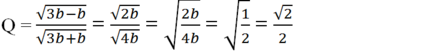
a) xác định a,b của (P) y=a2 +bx+c đi qua A(0;5) và có định I(3;4)
b)lập bảng biến thiên và vẽ p ở câu a
c) tìm tập hợp của giá trị x để y>0
d) tìm tập hợp của giá trị x để y<0
a: \(\left\{{}\begin{matrix}c=5\\\dfrac{-b}{2a}=3\\\dfrac{-\left(b^2-20a\right)}{4a}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=5\\b=-6a\\-\left(36a^2-20a\right)=16a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=5\\b=-6a\\36a^2-4a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{9}\\b=-6a=\dfrac{-2}{3}\\c=5\end{matrix}\right.\)
Câu 1. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)
Câu 2. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Câu 3. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.
Hãy giải ba câu hỏi này
Bài 2:
Ta có: M = a2+ab+b2 -3a-3b-3a-3b +2001
=> 2M = ( a2 + 2ab + b2) -4.(a+b) +4 + (a2 -2a+1)+(b2 -2b+1) + 3996
2M= ( a+b-2)2 + (a-1)2 +(b-1)2 + 3996
=> MinM = 1998 tại a=b=1
Câu 3:
Ta có: P= x2 +xy+y2 -3.(x+y) + 3
=> 2P = ( x2 + 2xy +y2) -4.(x+y) + 4 + (x2 -2x+1) +(y2 -2y+1)
2P = ( x+y-2)2 +(x-1)2+(y-1)2
=> MinP = 0 tại x=y=1
Bài1:
Ta có: a2+ b2+c2+d2= a.(b+c+d)
=> a2+b2+c2+d2 -ab -ac -ad =0
=> 4a2+ 4b2+4c2+4d2-4ab -4ac -4ad=0
=> ( a2 - 4ab +4b2) + ( a2- 4ac + 4c2) +( a2 -4ad+ 4d2) + a2=0
=> ( a-2b)2 + ( a-2c)2 + (a-2d)2 + a2 =0
=> ....
KL: a=b=c=d=0
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Cho phân thức M=(a2+b2+c2)(a+b+c)2+(ab+bc+ca)2 / (a+b+c)2-(ab+bc+ca)
a,Tìm các giá trị của a,b,c để phân thức được xác định(tức để mẫu ≠0)
b,Rút gọn M
Biết rằng đồ thị hàm số y = ( 3 a 2 - 1 ) x 3 - ( b 3 + 1 ) x 2 + 3 c 2 x + 4 d có hai điểm cực trị là (1;-7), (2:-8). Hãy xác định tổng M= a 2 + b 2 + c 2 + d 2 .
A. -18
B. 18
C. 15
D. 8
1. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức : M = a3 + b3.
2. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức : N = a + b.
3. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
4. Tìm liên hệ giữa các số a và b biết rằng: a b a b
5. a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8
6. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2) b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
7. Tìm các giá trị của x sao cho:
a) | 2x – 3 | = | 1 – x | b) x2 – 4x ≤ 5 c) 2x(2x – 1) ≤ 2x – 1.
8. Tìm các số a, b, c, d biết rằng : a2 + b2 + c2 + d2 = a(b + c + d)
9. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của avà b thì M đạt giá trị nhỏ nhất ? Tìm giá trị nhỏ nhất đó.
10. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. CMR giá trị nhỏ nhất của P bằng 0.
11. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau :
x2 + 4y2 + z2 – 2a + 8y – 6z + 15 = 0
bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....
bạn nên viết ra từng câu
Chứ để như thế này khó nhìn lắm
bạn hỏi từ từ thôi