ko biết

B = \(x^2\) - 2\(xy\) + 2y\(^2\) + 2\(x\) - 10y + 17

B = (\(x^2\) - 2\(xy\) + y²) + 2(\(x-y\)) + 1 + (y² - 8y + 16)

B = (\(x-y\))² + 2(\(x-y\)) + 1 + (y - 4)²

B = (\(x-y\) + 1)² + (y - 4)²

(\(x-y+1\))² ≥ 0 ∀ \(x;y\); (y - 4)² ≥ 0 

B ≥ 0

Kết luận biểu thức không âm. Chứ không phải là biểu thức luôn dương em nhé. Vì dương thì biểu thức phải > 0 ∀ \(x;y\). Mà số 0 không phải là số dương. 

Giải giúp mik với mik cần gấp

\(a,x^4-2x^3+6x^2+x+14\\ =\left(x^4-3x^3+7x^2\right)+\left(x^3-3x^2+7x\right)+\left(2x^2-6x+14\right)\\ =\left(x^2-3x+7\right)\left(x^2+x+2\right):\left(x^2-3x+7\right)=x^2+x+2\)

Ta có \(x^2+x+2=x^2+x+\dfrac{1}{4}+\dfrac{7}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}>0\)

Vậy ...

\(b,A=x^3+3xy+y^3\\ A=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\\ A=x^2-xy+y^2+3xy\\ A=x^2+2xy+y^2=\left(x+y\right)^2=1\)

\(B=x^2-2x+y^2+4y+6=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1>0\forall x,y\)

\(B=x^2-2x+y^2+4y+6\)

\(=x^2-2x+1+y^2+4y+4+1\)

\(=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1>0\forall x,y\)

cho hình thang cân , đáy nhỏ AB đáy lớn CD . Góc nhọn hợp từ hai đường chéo AC và BD bằng \(60^o\)gọi M,N là hình chiếu của B và C lên AC và BD , p là trung điểm cạnh BC . Cm tam giác MNP là tam giác đều

B=x^2-12x+6^2-8

=(x-6)^2-8

Biểu thức này ko thể luôn dương nha bạn

`A=x(x-6)+10=x^2-6x+10`

`=x^2 -2.x .3 + 3^2 + 1`

`=(x-3)^2+1 >0 forall x`

`B=x^2-2x+9y^2-6y+3`

`=(x^2-2x+1)+(9y^2-6y+1)+1`

`=(x-1)^2+(3y-1)^2+1 > 0 forall x,y`.

`B = x^2- 2xy + y^2 + 2x - 10y + 17

`2B = 2x^2 - 4xy + 2y^2 + 4x - 20y + 34`

`= (x-y)^2 + (x+2)^2 + (y-5)^2 + 5 >= 5`.

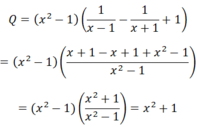
Do x2≥ 0 ∀ x ≠ ±1 nên Q=x2 + 1 ≥ 1 ∀ x ≠ ±1

a) \(A=y\left(x^2-y^2\right)\left(x^2+y^2\right)-y\left(x^4-y^4\right)=y\left(x^4-y^4\right)-y\left(x^4-y^4\right)=0\)

b) \(B=\left(x-1\right)^3-\left(x-1\right)\left(x^2+x+1\right)-3\left(1-x\right)x=x^3-3x^2+3x-1-x^3-x^2-x+x^2+x+1-3x+3x^2=0\)

a: Ta có: \(A=y\left(x^2-y^2\right)\left(x^2+y^2\right)-y\left(x^4-y^4\right)\)

\(=y\left(x^4-y^4\right)-y\left(x^4-y^4\right)\)

=0

b: Ta có: \(B=\left(x-1\right)^3-\left(x-1\right)\left(x^2+x+1\right)-3x\left(1-x\right)\)

\(=x^3-3x^2+3x-1-x^3+1-3x+3x^2\)

=0