Cho hình vẽ. Chứng minh Bx // Cy 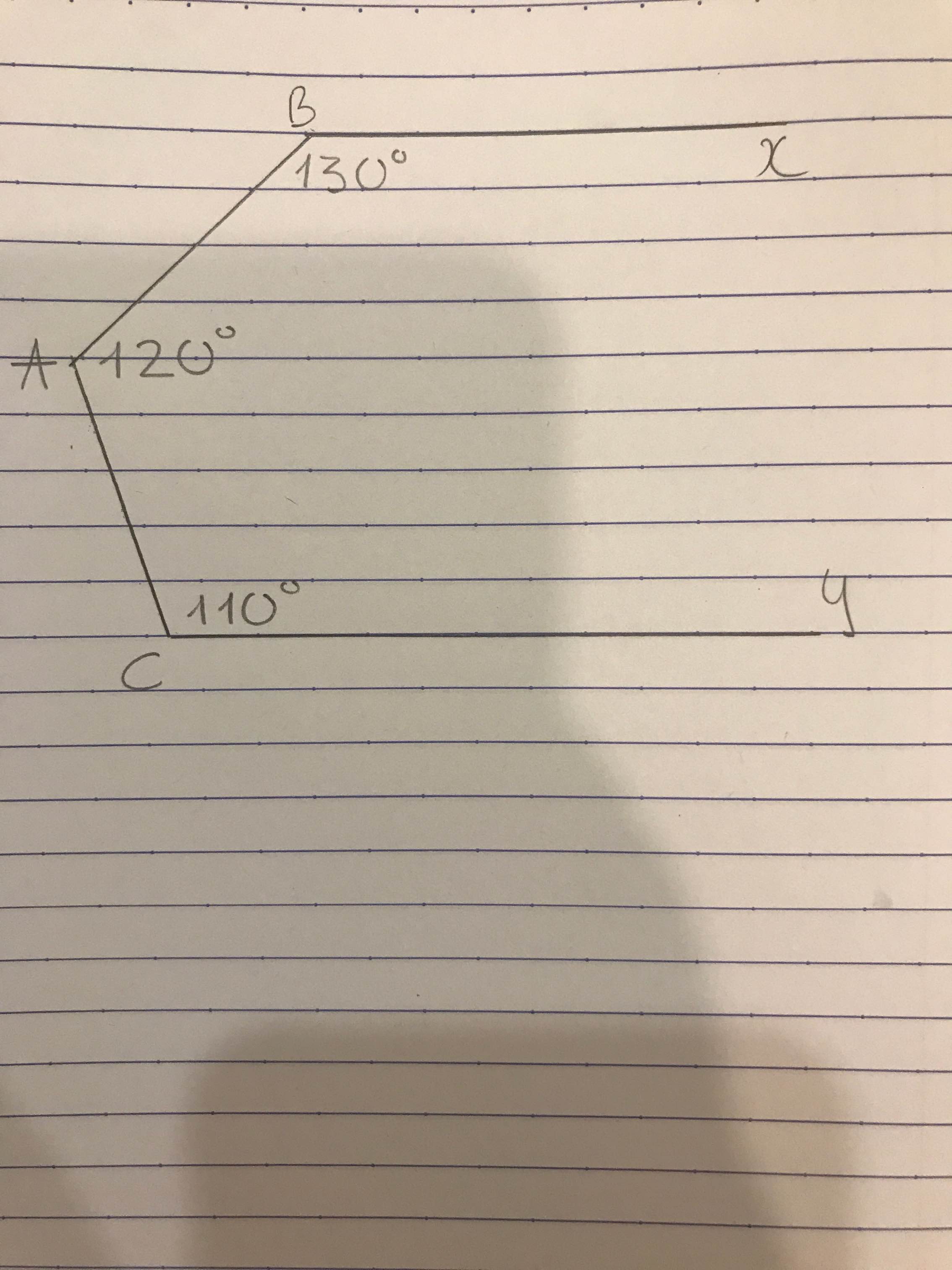
HS
Những câu hỏi liên quan
cho tam giác ABC vuông tại A có E,K lần lượt là trung điểm của AB,AC a) chứng minh EK//BC b) Từ B vẽ tia Bx song song với AC, từ C vẽ tia Cy song song với AB. Tia Bx và Cy cắt nhau tại M. Chứng minh tứ giác ABMC là hình chữ nhật. c) Từ K vẽ đường thẳng song song với AB cắt BC tại O. Chứng minh 3 điểm A,O,M thẳng hàng.
Đọc tiếp
cho tam giác ABC vuông tại A có E,K lần lượt là trung điểm của AB,AC a) chứng minh EK//BC b) Từ B vẽ tia Bx song song với AC, từ C vẽ tia Cy song song với AB. Tia Bx và Cy cắt nhau tại M. Chứng minh tứ giác ABMC là hình chữ nhật. c) Từ K vẽ đường thẳng song song với AB cắt BC tại O. Chứng minh 3 điểm A,O,M thẳng hàng.
Hình Tự Vẽ nhe
a)
Tam Giác ABC có:
E là trung điểm của AB (gt)
K là trung điểm của AC(gt)
=> EK là đường trung bình của tam giác ABC
=> EK//BC ( tính chất đường trung bình của tam giác )
b)
Tứ giác ABMC có:
BM//AC ( Bx//AC; M thuộc Bx)
CM//AB ( Cy//AB; M thuộc Cy )
Góc A = 90 độ (gt)
=> tứ giác ABMC là Hình chữ nhật
=> AB//MC (tính chất hình chữ nhật )
c)
Ta có: AB // KO ( Từ K vẽ đường thẳng song song với AB cắt BC tại O )
mà AB//MC(cmt) => MC//KO
Tam Giác ABC có:
K là trung điểm của AC (gt)
KO // AB ( Từ K vẽ đường thẳng song song với AB cắt BC tại O )
=> KO là đường trung bình của tam giác ABC
=> O là trung điểm của BC ( tính chất đường trung bình trong tam giác )
tam giác AMC có:
K là trung điểm của AC (gt)
KO//MC (cmt)
=> KO là đường trung bình của tam giác AMC => O là trung điểm của AM ( tính chất đường trung bình trong tam giác )
Vì tứ giác ABMC là Hình chữ nhật => AM Cắt BC tại trung điểm của Mỗi đường mà O là trung điểm của AM và BC => AM cắt BC tại O => A;M;O Thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A , vẽ tia Bx và Cy lần lượt vuông góc AB và AC sao cho Bx cắt Cy tại D (D và A nằm hai phía của đường thẳng BC). Chứng minh:
a)Tứ giác ABCD là hình chữ nhật.
b)Tứ giác ABCD có là hình vuông không ? vì sao ?
c)Chứng minh: AD vuông góc BC.
Cho tam giác ABC vuông cân tại A , vẽ tia Bx và Cy lần lượt vuông góc AB và AC sao cho Bx cắt Cy tại D (D và A nằm hai phía của đường thẳng BC). Chứng minh:
a)Tứ giác ABCD là hình chữ nhật.
b)Tứ giác ABCD có là hình vuông không ? vì sao ?
c)Chứng minh: AD vuông góc BC
Cho góc BAC, vẽ 2 tia Bx và Cy nằm bên ngoài góc BAC sao cho góc BAC= ABx + ACy. Chứng minh Bx//Cy
Bài 4: Cho DABC vuông cân tại A , vẽ tia Bx và Cy lần lượt vuông góc AB và AC sao cho Bx cắt Cy tại D (D và A nằm hai phía của đường thẳng BC). Chứng minh:a)Tứ giác ABCD là hình chữ nhật.b)Tứ giác ABCD có là hình vuông không ? vì sao ?c)Chứng minh: AD^BC.Bài 5: Cho ∆ABC (A90o) có AB AC. Gọi M là trung điểm của BC. Vẽ MD vuông gócvới AB tại D và ME vuông góc với AC tại E. Vẽ đường cao AH của ∆ABC.a) Chứng minh ADME là hình chữ nhật.b) Chứng minh CMDE là hình bình hành.c) Chứng minh MHDE là hình...
Đọc tiếp
Bài 4: Cho DABC vuông cân tại A , vẽ tia Bx và Cy lần lượt vuông góc AB và AC sao cho Bx cắt Cy tại D (D và A nằm hai phía của đường thẳng BC). Chứng minh:
a)Tứ giác ABCD là hình chữ nhật.
b)Tứ giác ABCD có là hình vuông không ? vì sao ?
c)Chứng minh: AD^BC.
Bài 5: Cho ∆ABC (A=90o) có AB < AC. Gọi M là trung điểm của BC. Vẽ MD vuông góc
với AB tại D và ME vuông góc với AC tại E. Vẽ đường cao AH của ∆ABC.
a) Chứng minh ADME là hình chữ nhật.
b) Chứng minh CMDE là hình bình hành.
c) Chứng minh MHDE là hình thang cân.
Bài 6: Cho DABC cân tại A có AB = 3cm, BC= \(3\sqrt{2}cm\), D là điểm đối xứng với A qua BC.
a)Chứng minh DABC vuông cân tại A.
b)Chứng minh tứ giác ABCD là hình bình hành.
c)Hình bình hành ABCD có hình vuông không ? Vì sao ?
Cho tam giác ABC vuông tại A. Qua B kẻ Bx vuông góc với AB, qua C kẻ Cy vuông góc AC. Gọi D là giao điểm của Bx và Cy.
a) Chứng minh tứ giác ABDC là hình chữ nhật.
b) Vẽ M đối xứng với B qua A, N đối xứng với C qua A. Chứng minh tứ giác BCMN là hình thoi và AD = MC.
c) Gọi E, F thứ tự là trung điểm của AC và MN. Chứng minh EF// ND.
a) Để chứng minh tứ giác ABDC là hình chữ nhật, ta cần chứng minh AB || CD và AB = CD.
Vì Bx vuông góc với AB, nên AB || Bx.
Vì Cy vuông góc với AC, nên AC || Cy.
Do đó, AB || CD.
Ta có:
- Góc ABC = 90 độ (vì tam giác ABC vuông tại A).
- Góc BAC = 90 độ (vì Bx vuông góc với AB).
- Góc ACB = 90 độ (vì Cy vuông góc với AC).
Vậy tứ giác ABDC có 4 góc vuông, tức là là hình chữ nhật.
b) Gọi M là điểm đối xứng của B qua A và N là điểm đối xứng của C qua A. Ta cần chứng minh tứ giác BCMN là hình thoi và AD = MC.
Vì M là điểm đối xứng của B qua A, nên AM = MB và góc AMB = góc BMA = 90 độ.
Vì N là điểm đối xứng của C qua A, nên AN = NC và góc ANC = góc CNA = 90 độ.
Do đó, ta có:
- AM = MB = MC (vì M là trung điểm của BC).
- AN = NC = NB (vì N là trung điểm của BC).
- Góc BMC = góc BMA + góc AMC = 90 độ + 90 độ = 180 độ (tổng các góc trong tứ giác là 360 độ).
Vậy tứ giác BCMN là hình thoi và AD = MC.
c) Gọi E là trung điểm của AC và F là trung điểm của MN. Ta cần chứng minh EF || ND.
Vì E là trung điểm của AC, nên AE = EC.
Vì F là trung điểm của MN, nên AF = FN.
Do đó, ta có:
- AE = EC = AF = FN.
- Góc AEF = góc AFE = góc NDF = góc NFD = 90 độ (vì E và F lần lượt là trung điểm của AC và MN).
Vậy EF || ND.
Đúng 0
Bình luận (0)
Cho ∆ ABC nhọn. Đường cao AD, BE, CF cắt nhau tại H. Vẽ tia Bx vuông góc với tia AB, tia Cy vuông góc với tia AC. Biết Bx và Cy cắt tại M. a) Chứng minh BHCN là hình bình hành b) Gọi OIK theo thứ tự là trung điểm của AM, BC, AC. Chứng minh 3 điểm thẳng hàng c) Chứng minh ∆OIK ~ ∆HAB
giúp em với ạ e đg cần gấp ạ e c.ơn❤️
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn , đường cao BH và CK cắt nhau tại e . Qua B vẽ đường thẳng Bx vuông góc AB , qua C vẽ Cy vuông với AC . Hai đường Bx và Cy cắt nhau tại D
a.chứng minh BDCE là hình gì
b.gọi M là trung điểm BC . Chứng minh MD bằng ME
Nhớ vẽ hình dùm mình nghe đang cần gắp
Cho tam giác ABC nhọn có hai đường cao BE và CF cắt nhau tại
H (E thuộc cạnh AC, F thuộc cạnh AB). Qua B vẽ Bx vuông góc với AB, qua C vẽ Cy vuông góc AC, Bx cắt Cy tại D.
a) Chứng minh tứ giác BHCD là hình bình hành.
b) Gọi M là trung điểm của BC. Chứng minh H, M, D thẳng hàng.
c) Gọi O là trung điểm AD. Chứng minh OB = OC.
d) Chứng minh OA=OB=OC=OD
a: Xét tứ giác BHCD có
BH//CD
CH//BD
Do đó:BHCD là hình bình hành
b: Ta có: BHCD là hình bình hành
nên Hai đường chéo BC và HD cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HD
hay H,M,D thẳng hàng
Đúng 0
Bình luận (0)



