Cho hình vẽ , Ax // By , Tính A + B + C
LS
Những câu hỏi liên quan
Cho hình vẽ biết Cz//Ax,góc c=30°,góc ACB=110° a)chứng minh Ax//By,Cz//By b)tính góc CBy c)tính số đo góc acd
Giúp tui với mn ơi cần gấp lắm ròi :<
Đúng 0
Bình luận (0)
Cho hình vẽ, chứng minh: Ax song song By ( Ax//By )
c B A y x 124* 56*
Đọc tiếp
Cho hình vẽ, chứng minh: Ax song song By ( Ax//By )
Lời giải:
Ta thấy:
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)
Đúng 0
Bình luận (0)
Cho hình vẽ bên, biết Ax//By, góc A bằng 20o, góc B bằng 120o. Tính số đo x (góc C)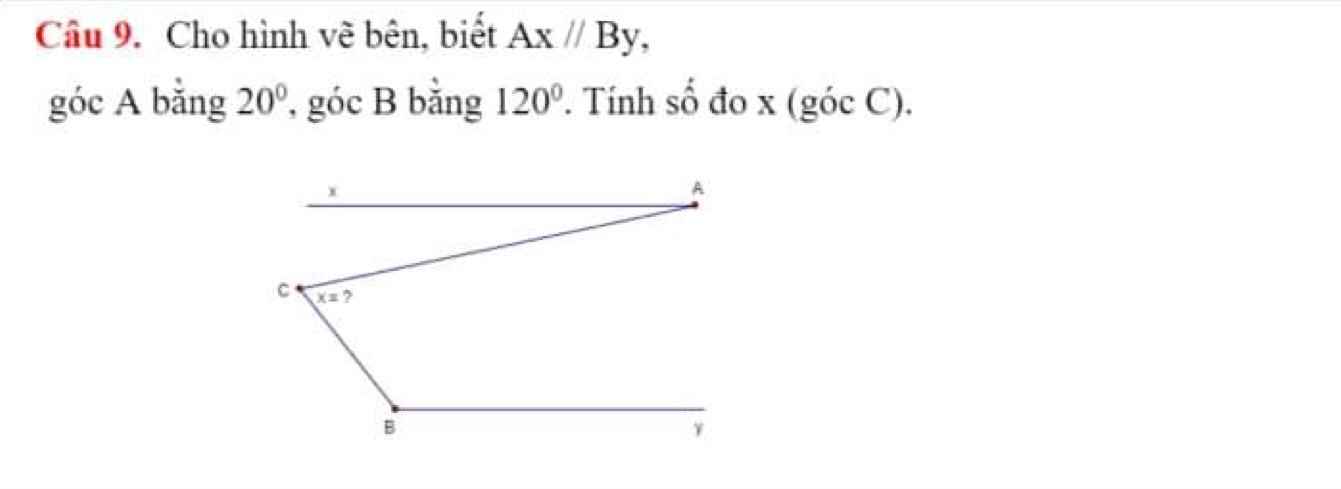
Cho hình vẽ biết Ax//By. Tính <BAx+<ABC+<BOy
Biết <A + <B + <C = 360 độ
CMR:Ax//By
Cho hình vẽ:
45* 135* 75* 30* A x B C y z
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz
Đọc tiếp
Cho hình vẽ:
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz

a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
Đúng 0
Bình luận (0)
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA a, OB b (a,b cùng đơn vị: cm).Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).Tính diện tích hình thang ABCD khi
C
O
A
^
60
o
Đọc tiếp
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA = a, OB = b (a,b cùng đơn vị: cm).
Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).
Tính diện tích hình thang ABCD khi C O A ^ = 60 o
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA a, OB b (a,b cùng đơn vị: cm).Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).Với
C
O
A
^
60
o
cho hình vẽ quay xung quanh AB. Tính tỉ số thể tích các hình do các tam giác AOC và BOD tạo thành.
Đọc tiếp
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA = a, OB = b (a,b cùng đơn vị: cm).
Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).
Với C O A ^ = 60 o cho hình vẽ quay xung quanh AB. Tính tỉ số thể tích các hình do các tam giác AOC và BOD tạo thành.
Khi quay hình vẽ xung quanh cạnh AB: ΔAOC tạo nên hình nón, bán kính đáy là AC, chiều cao AO; ΔBOD tạo nên hình nón, bán kính đáy BD, chiều cao OB.

Đúng 0
Bình luận (0)
a) Cho hình vẽ, biết Ax //By ,goc A 30độ,gócAOB 70 độ. Tính góc B b) Cho hình vẽ, biết Góc A 60 độ,góc B 40 độ. tính số đo x,y
Đọc tiếp
a) Cho hình vẽ, biết Ax //By ,goc A= 30độ,gócAOB= 70 độ. Tính góc B
b) Cho hình vẽ, biết Góc A= 60 độ,góc B= 40 độ. tính số đo x,y
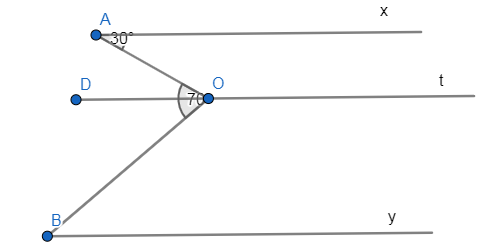
a, Kẻ Ot sao cho Ot song song với Ax và By, ta có:
\(\widehat{xAO}=\widehat{AOD}\) (So le trong)
\(\Rightarrow\widehat{xAO}=\widehat{AOD}=30^0\\\Rightarrow\widehat{DOB}=70^0-30^0=40^0\)
Mà OD//By
\(\Rightarrow\widehat{B}=\widehat{DOB}=40^0\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn nửa đường thẳng Ax, By, Cz, Dt ở cùng phía đối với mặt phẳng (ABCD), song song với nhau và không nằm trong mặt phẳng (ABCD). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz và Dt tại A’, B’, C’ và D’.a) Chứng minh: mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt)b) Gọi I AC ∩ BD, J A’C’ ∩ B’D’. Chứng minh: IJ song song với AA’.c) Cho AA’ a, BB’ b, CC’ c. Hãy tính DD’.
Đọc tiếp
Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn nửa đường thẳng Ax, By, Cz, Dt ở cùng phía đối với mặt phẳng (ABCD), song song với nhau và không nằm trong mặt phẳng (ABCD). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz và Dt tại A’, B’, C’ và D’.
a) Chứng minh: mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt)
b) Gọi I = AC ∩ BD, J = A’C’ ∩ B’D’. Chứng minh: IJ song song với AA’.
c) Cho AA’ = a, BB’ = b, CC’ = c. Hãy tính DD’.
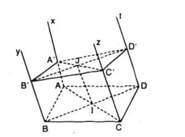
a) Do ABCD là hình bình hành, nên AB // DC
=> AB // (Cz, Dt) (1)
Theo giả thiết Ax // Dt nên Ax // (Cz, Dt) (2)
Từ (1) và (2) suy ra: (Ax, By) // (Cz, Dt)
b) Mặt phẳng β cắt 2 mặt phẳng song song ( Ax, By), (Cz, Dt) theo hai giao tuyến là A’B’và C’D’ nên A’B’// C’D’. (3)
Chứng minh tương tự (Ax, Dt) song song với (By,Cz).Và mặt phẳng β cắt 2 mặt phẳng song song (Ax, Dt), (By, Cz) theo hai giao tuyến là A’D’và B’C’ nên A’D’// B’C’ (4)
Từ (3) và (4) suy ra: tứ giác A’B’C’D’ là hình bình hành.
=> J là trung điểm của A’C’ ( tính chất hình bình hành).
Tứ giác AA’C’C là hình thang vì có: AA’ // CC’ ( giả thiết). Lại có, I và J lần lượt là trung điểm của AC và A’C’ nên IJ là đường trung bình của hình thang
=> IJ// AA’// CC’ ( đpcm).
c) Vì IJ là đường trung bình của hình thang ACC’A’ nên IJ = 1/2(AA’ + CC’)
IJ cũng là đường trung bình của hình thang BDD’B’: IJ = 1/2(BB’ + DD’)
Từ đây suy ra: DD’ + BB’ = AA’ + CC’
=> DD’ = AA’ + CC’ – BB’ = a + c – b
Đúng 0
Bình luận (0)
Cho ba điểm A, O, B thẳng hàng, OA a, OB b (a, b cùng đơn vị là cm). Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở Da, Chứng minh các tam giác AOC và BDO đồng dạng. Từ đó suy ra tích AC.BD không đổib, Với
C
O
A
^
60
0...
Đọc tiếp
Cho ba điểm A, O, B thẳng hàng, OA = a, OB = b (a, b cùng đơn vị là cm). Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D
a, Chứng minh các tam giác AOC và BDO đồng dạng. Từ đó suy ra tích AC.BD không đổi
b, Với C O A ^ = 60 0 , hãy:
i, Tính diện tích hình thang ABCD
ii, Tính tỉ số thể tích các hình do các tam giác AOC và BOD tạo thành khi cho hình vẽ quay xung quanh AB
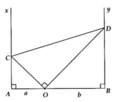
a, A O C ^ = O D B ^ (cùng phụ B O D ^ )
=> DAOC ~ DBDO (g.g)
=> A C B O = A O B D
=> AC.BD = a.b (không đổi)
b, Ta có C O A ^ = O D B ^ = 60 0 , A C O ^ = D O B ^ = 30 0 , AC = a 3 , BD = b 3 3
i, S A B C D = 3 a + b 3 a + b 6
ii, 9
Đúng 0
Bình luận (0)





