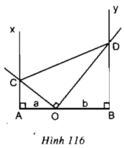
Cho ba điểm A, O, B thẳng hàng, OA = a, OB = b (a, b cùng đơn vị là cm). Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D
a, Chứng minh các tam giác AOC và BDO đồng dạng. Từ đó suy ra tích AC.BD không đổi
b, Với C O A ^ = 60 0 , hãy:
i, Tính diện tích hình thang ABCD
ii, Tính tỉ số thể tích các hình do các tam giác AOC và BOD tạo thành khi cho hình vẽ quay xung quanh AB
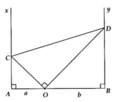
a, A O C ^ = O D B ^ (cùng phụ B O D ^ )
=> DAOC ~ DBDO (g.g)
=> A C B O = A O B D
=> AC.BD = a.b (không đổi)
b, Ta có C O A ^ = O D B ^ = 60 0 , A C O ^ = D O B ^ = 30 0 , AC = a 3 , BD = b 3 3
i, S A B C D = 3 a + b 3 a + b 6
ii, 9