Bài 19. Cho hình vẽ, biết D= 1230, E = 1370 và F = 1000.
H24
Những câu hỏi liên quan
Cho hình vẽ. Biết
A
^
123
0
,
B
^
57
0
và
d
⊥
a
.
Hỏi d có vuông góc với b không?
Đọc tiếp
Cho hình vẽ. Biết A ^ = 123 0 , B ^ = 57 0 và d ⊥ a . Hỏi d có vuông góc với b không?
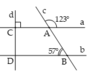
C A B ^ + A B D ^ = 180 0 ⇒ a // b
Mà d ⊥ a ⇒ d ⊥ b . Do đó d ⊥ a .
Đúng 0
Bình luận (0)
Bài 23. Vẽ điểm D và E sao cho D nằm giữa C và E còn E nằm giữa D và F. a) Vì sao có thể khẳng định 4 điểm C, D, E, F thẳng hàng. b) Kể tên hai tia trùng nhau gốc E. c) Vì sao có thể khẳng định điểm E nằm giữa C và F. Bài 24. Em hãy cho biết có thể vẽ được bao nhiêu đường thẳng phân biệt đi qua các cặp điểm trong mỗi trường hợp sau: a) Với hai điểm phân biệt cho trước. b) Với ba điểm phân biệt cho trước và không thẳng hàng. c) Với bốn điểm phân biệt cho trước, trong đó không có ba điểm nào thẳng...
Đọc tiếp
Bài 23. Vẽ điểm D và E sao cho D nằm giữa C và E còn E nằm giữa D và F. a) Vì sao có thể khẳng định 4 điểm C, D, E, F thẳng hàng. b) Kể tên hai tia trùng nhau gốc E. c) Vì sao có thể khẳng định điểm E nằm giữa C và F. Bài 24. Em hãy cho biết có thể vẽ được bao nhiêu đường thẳng phân biệt đi qua các cặp điểm trong mỗi trường hợp sau: a) Với hai điểm phân biệt cho trước. b) Với ba điểm phân biệt cho trước và không thẳng hàng. c) Với bốn điểm phân biệt cho trước, trong đó không có ba điểm nào thẳng hàng. d) Với 10 điểm phân biệt cho trước, trong đó không có ba điểm nào thẳng hàng. e) Với n điểm phân biệt cho trước, trong đó không có ba điểm nào thẳng hàng.
Bài 4: Cho hình vẽ bên Biết rằng D,E,F,G lần lượt là trung điểm của AB, AC, DE, BC. Cmr: A, F, G thẳng hàng
hình cuối
Cho hàm số y f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y f( x) trên [ a; e]? A.
m
a
x
[
a
,...
Đọc tiếp
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f( x) trên [ a; e]?
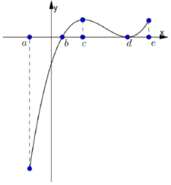
A. m a x [ a , e ] f ( x ) = f ( c ) m i n [ a , e ] f ( x ) = f ( a )
B. m a x [ a , e ] f ( x ) = f ( a ) m i n [ a , e ] f ( x ) = f ( b )
C. m a x [ a , e ] f ( x ) = f ( e ) m i n [ a , e ] f ( x ) = f ( b )
D. m a x [ a , e ] f ( x ) = f ( d ) m i n [ a , e ] f ( x ) = f ( b )
Ta có bảng biến thiên như hình vẽ sau:
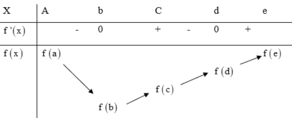
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.
Đúng 0
Bình luận (0)
Cho hình H tạo bởi hình chữ nhật ABCD và hình bình hành BEFC như hình vẽ bên.Tính diện tích hình H.Hình này bạn nào làm cả bài giải thì mình tk cho 3cm D C F A B E 4cm 3cm
Diện tích của hình chữ nhật ABCD là :
4 x 3 = 12 ( cm2 )
Diện tích của hình bình hành BEFC là :
4 x 3 = 12 ( cm2 )
Diện tích của hình H là :
12 + 12 = 24 (cm2 )
Đ/S : 24 cm2
3P
21 tháng 2 2022 lúc 19:07
Cho ∆ABC cân tại A. Gọi D là trung điểm của BC. Vẽ DE vuông góc AB tại E, vẽ DF vuông góc AC tại F. Chứng minh:
a/ ∆DEB = ∆DFC.
b/ ∆AED = ∆AFD.
c/ AD là phân giác góc BAC.
Mong mụi ngừ giúp e làm bài này và vẽ hình giúp e lun ạ..! <3 =))❤
a, Xét tam giác DEB và tam giác DFC ta có
BD = DC (gt)
^B = ^C (gt)
Vậy tam giác DEB = tam giác DFC (ch-gn)
=> DE = DF ( 2 cạnh tương ứng )
b, Xét tam giác AED và tam giác AFD có
AD _ chung
DE = DF (cmt)
Vậy tam giác AED = tam giác AFD (ch-cgv)
=> ^EAD = ^FAD ( góc tương ứng )
b, Xét tam giác ABC có
^EAD = ^FAD (cmt) hay AD là phân giác ^A
Đúng 1
Bình luận (1)
Bài 19: Cho ΔABC đều, M là điểm bất kỳ thuộc cạnh BC. E,F lần lượt là chân đường vuông góc kẻ từ M đến AB,AC. I và D lần lượt là trung điểm của AM,BC.
a, Cm I cách đều 3 điểm D,F,E
b, Tính số đo DIE
c, Cm DEIF là hình thoi
a: góc ADM=góc AFM=góc AEM=90 độ
=>A,E,D,M,F cùng thuộc đường tròn đường kính AM
=>I là tâm đường tròn ngoại tiếp đa giác AEMDF
=>I cách đều D,F,E
b:
ΔABC đều
mà AD là đường trung tuyến
nên AD là phân giác của góc BAC
=>góc BAD=góc CAD=30 độ
Xét (I) có
góc EAD là góc nội tiếp chắn cung ED
=>góc EAD=1/2*sđ cung ED
=>1/2*sđ cung ED=30 độ
=>sđ cung ED=60 độ
=>góc DIE=60 độ
Đúng 0
Bình luận (0)
Bài 2: Cho tam giác nhọn ABC. Gọi D, E, F lần lượt là trung điểm của AB, AC và BC. Vẽ điểm I sao cho D là trung điểm của IF.
a) CM: tứ giác BDEC là hình thang; b) CM: tứ giác AEFD, AFBI là hình bình hành.
a: Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và DE=1/2BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
b: Xét tứ giác AFBI có
D là trung điểm chung của AB và FI
=>AFBI là hình bình hành
Xét ΔABC có
F,D lần lượt là trung điểm của BC,BA
=>FD là đường trung bình của ΔABC
=>FD//AC và \(FD=\dfrac{AC}{2}\)
Ta có: FD//AC
E\(\in\)AC
Do đó: FD//AE
Ta có: \(FD=\dfrac{AC}{2}\)
\(AE=\dfrac{CA}{2}\)
Do đó: FD=AE
Xét tứ giác ADFE có
DF//AE
DF=AE
Do đó: ADFE là hình bình hành
Đúng 0
Bình luận (0)