cho tam giác abc có đỉnh a(0;4) ,trọng tâm G (4/3;2/3) và trực tâm trùng với gốc tọa độ.tìm b,c biết xb<xc
TT
Những câu hỏi liên quan
Cho tam giác ABC có các đỉnh A(0;-3), B(1;1), C(3;2). Khi đó, đường cao của tam giác vẽ từ đỉnh A có phương trình:
A. 2x - y - 2 = 0
B. x - 2y - 6 = 0
C. 2x + y + 3 = 0
D. x + 2y - 8 = 0
Đáp án: C
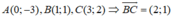
Đường cao kẻ từ A của tam giác ABC là đường thẳng đi qua A và nhận vecto BC là vecto pháp tuyến
⇒ d: 2(x - 0) + (y + 3) = 0 ⇔ 2x + y + 3 = 0
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho tam giác ABC có tọa độ các đỉnh là:
A(a; 0; 0), B(0; b; 0), C(0; 0; c)
Chứng minh rằng tam giác ABC có ba góc nhọn.
Ta có: AB → = (−a; b; 0) và AC → = (−a; 0; c)
Vì AB → . AC → = a 2 > 0 nên góc ∠ BAC là góc nhọn.
Lập luận tương tự ta chứng minh được các góc ∠ B và ∠ C cũng là góc nhọn.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn có phương trình
x
2
+
y
2
–
4
x
-
2
y
–
8
0
. Đỉnh A thuộc tia Oy, đường cao kẻ từ đỉnh C thuộc đường thẳng x + 5y 0. Tìm tọa độ đỉnh B của tam giác ABC. A. B (-1;-1) B. B (0;4...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn có phương trình x 2 + y 2 – 4 x - 2 y – 8 = 0 . Đỉnh A thuộc tia Oy, đường cao kẻ từ đỉnh C thuộc đường thẳng x + 5y = 0. Tìm tọa độ đỉnh B của tam giác ABC.
A. B (-1;-1)
B. B (0;4)
C. B (5;-1)
D. B (1;9)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn có phương trình
x
2
+
y
2
–
4
x
-
2
y
–
8
0
. Đỉnh A thuộc tia Oy, đường cao kẻ từ đỉnh C thuộc đường thẳng x + 5y 0. Tìm tọa độ đỉnh B của tam giác ABC. A. B (-1;-1) B. B (0;4...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn có phương trình x 2 + y 2 – 4 x - 2 y – 8 = 0 . Đỉnh A thuộc tia Oy, đường cao kẻ từ đỉnh C thuộc đường thẳng x + 5y = 0. Tìm tọa độ đỉnh B của tam giác ABC.
A. B (-1;-1)
B. B (0;4)
C. B (5;-1)
D. B (1;9)
Câu 26 . Cho tam giác ABC. Biết A(4;3), trọng tâm G(1;1), trực tâm H( 104/3;-20) XB > 0. Tìm tọa độ hai đỉnh B,CCâu 27. Cho tam giác ABC có A(0; 2), hai đường trung tuyến BM : 4x + 3y – 10 = 0; CN : x – 2 = 0 . Tọa độ các đỉnh B;C là:
Xem chi tiết
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1;-3), phương trình đường phân giác trong đỉnh B là x+y-2=0 và phương trình đường trung tuyến hạ từ đỉnh C là x+8y-7=0. Tìm tọa độ các đỉnh B và C của tam giác ABC
goi B(a; b) N( c; d)
\(N\in\left(CN\right)\Rightarrow\)c+8d-7 = 0(1)
N la trung diem AB\(\Rightarrow2c=1+a\left(2\right)\)
2d = -3 +b (3)
B\(\in\left(BM\right)\)\(\Rightarrow\)a+b -2 =0 (4)
tu (1) (2) (3) (4) \(\Rightarrow a=-5;b=7\Rightarrow B\left(-5;7\right)\)
dt (AE) qua vuong goc BM. \(\Rightarrow pt\)(AE):x-y-4 = 0
tọa độ H \(\left\{{}\begin{matrix}x-y-4=0\\x+y-2=0\end{matrix}\right.\Rightarrow H\left(3;-1\right)\);H là trung điểm AE
\(\Rightarrow E\left(5;1\right)\). vì ptdt (BE) cung la ptdt qua (BC):
3x+5y-20 =0
tọa độ C là nghiệm hệ \(\left\{{}\begin{matrix}3x+5y-20=0\\x+8y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{139}{21}\\\dfrac{1}{21}\end{matrix}\right.\)
\(\Rightarrow C\left(\dfrac{139}{21};\dfrac{1}{21}\right)\)
Đúng 0
Bình luận (0)
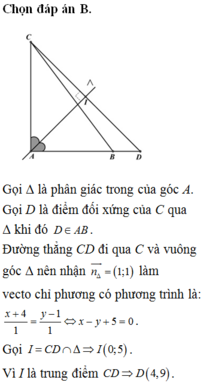
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-50. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B. A. B(4;-5) B. B(4;7) C. B(4;5) D. B(4;-7)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-5=0. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
A. B(4;-5)
B. B(4;7)
C. B(4;5)
D. B(4;-7)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-50. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-5=0. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
![]()
![]()
![]()
![]()
Trong mặt phẳng với hệ tọa độ oxy , cho tam giác ABC có đỉnh A(4-1) phương trình đường cao và trung tuyến kẻ từ đỉnh B lần lượt là 2x-3y+12=0 và 3 và 2x-3y=0. Xác định tọa độ các đỉnh còn lại của tam giác ABC
Bạn coi lại đề, 2 đường thẳng xuất phát từ B nhưng lại song song với nhau, điều này hoàn toàn vô lý
Đúng 0
Bình luận (0)
Cho tam giác ABC có đỉnh A(1;3) và 2 trung tuyến có phương trình x-2y+1=0, y=1. Lập phương trình các cạnh của tam giác ABC
Thay tọa độ A vào 2 pt trung tuyến đều không thỏa mãn
\(\Rightarrow\) 2 trung đó đó xuất phát từ B và C, giả sử trung tuyến xuất phát từ B có pt x-2y+1=0 và từ C có pt y=1
\(\Rightarrow B\left(2b-1;b\right)\) ; \(C\left(c;1\right)\)
Gọi G là trọng tâm tam giác \(\Rightarrow\) G là giao điểm 2 trung tuyến nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x-2y+1=0\\y=1\end{matrix}\right.\) \(\Rightarrow G\left(1;1\right)\)
Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}1+2b-1+c=3.1\\3+b+1=3.1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2b+c=3\\b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-1\\c=5\end{matrix}\right.\)
\(\Rightarrow B\left(-3;-1\right)\) ; \(C\left(5;1\right)\)
Biết 3 tọa độ 3 đỉnh của tam giác, dễ dàng viết được phương trình các cạnh
Đúng 2
Bình luận (0)