Giải chi tiết giúp mình với !!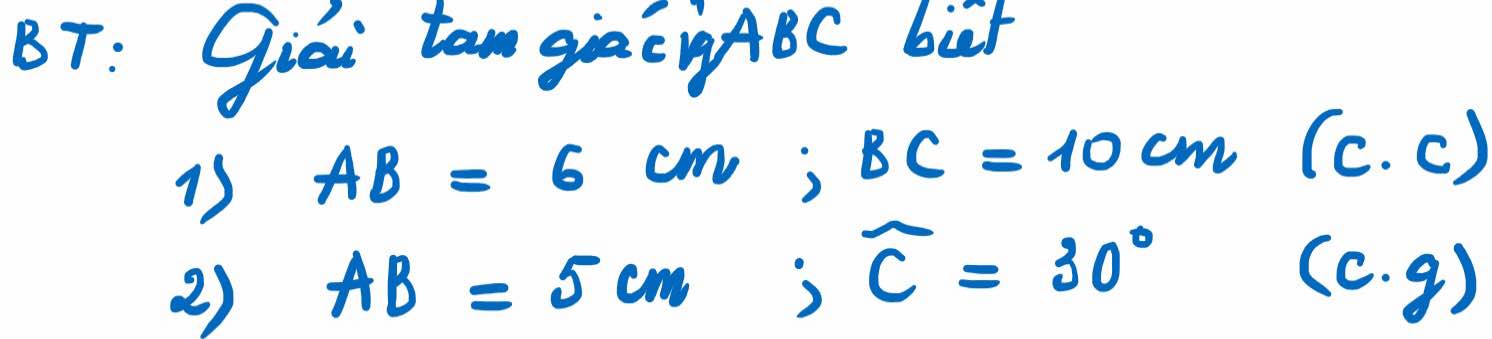
TT
Những câu hỏi liên quan
Giải giúp mình bài này với ạ giải câu c chi tiết xíu giúp mình với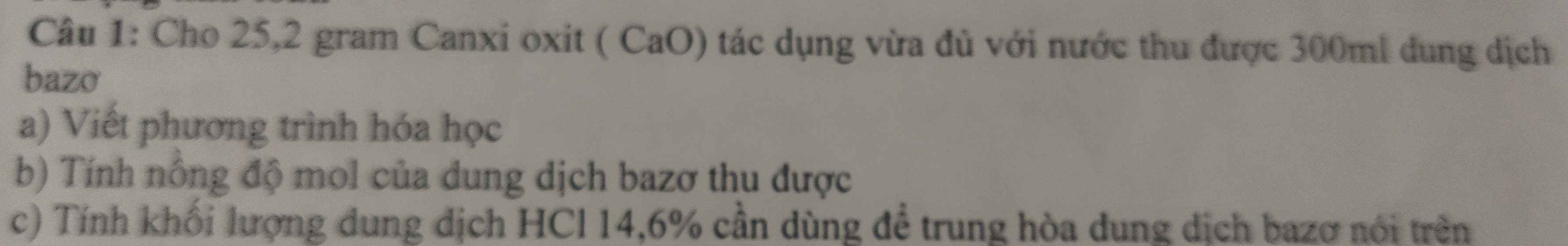
Giúp mình với ạ! Khi giải ghi lời giải chi tiết giúp mình nka 💜💜
Fe3O4 + 3H2 -> 3Fe + 4H2O
232 3\(\times\)56 (M)
\(mFe3O4=1.5\times80\%=1.2\) tấn
\(mFe=\dfrac{1.2\times3\times56}{232}=0.87\) tấn
Chọn D
Đúng 3
Bình luận (0)
Giúp mình giải chi tiết câu cuối hoặc định hướng giúp mình cách giải với ạ!
Giúp mình với ạ, giải chi tiết giúp mình nha mình cảm ơn nhiều!!
Giải giúp mình với giải hết chi tiết ak
6:
=0,25(2+3+5)*1-1=2,5-1=1,5
Đúng 0
Bình luận (0)
Giải chi tiết giúp mình với, mình cần gấp


giải chi tiết giúp mình với mình cảm ơn
Đọc tiếp
giải chi tiết giúp mình với mình cảm ơn
Giải chi tiết giúp mình với 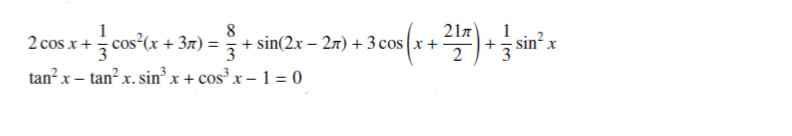
a.
Công thức góc cơ bản: \(cos\left(a+k\pi\right)=\pm cosa\) ; \(sin\left(a+k2\pi\right)=sina\) ; \(cos\left(a+\dfrac{\pi}{2}\right)=-sina\)
Do đó pt tương đương:
\(2cosx+\dfrac{1}{3}cos^2x=\dfrac{8}{3}+sin2x-3sinx+\dfrac{1}{3}sin^2x\)
\(\Leftrightarrow6cosx+1-sin^2x=8+3sin2x-9sinx+sin^2x\)
\(\Leftrightarrow2sin^2x-9sinx+7+6sinx.cosx-6cosx=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2sinx-7\right)+6cosx\left(sinx-1\right)=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2sinx+6cosx-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\\2sinx+6cosx=7\left(1\right)\end{matrix}\right.\)
Xét (1), ta có \(2^2+6^2=40< 7^2\) nên (1) vô nghiệm
Vậy họ nghiệm của pt là \(x=\dfrac{\pi}{2}+k2\pi\)
Đúng 0
Bình luận (0)
b.
Ta có:
\(tan^2x\left(1-sin^3x\right)+cos^3x-1=0\)
\(\Leftrightarrow\dfrac{\left(1-cos^2x\right)\left(1-sin^3x\right)}{\left(1-sin^2x\right)}-\left(1-cos^3x\right)=0\)
\(\Leftrightarrow\dfrac{\left(1-cosx\right)\left(1+cosx\right)\left(1+sinx+sin^2x\right)}{1+sinx}-\left(1-cosx\right)\left(1+cosx+cos^2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\Rightarrow x=k2\pi\\\dfrac{\left(1+cosx\right)\left(1+sinx+sin^2x\right)}{1+sinx}=1+cosx+cos^2x\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Rightarrow\left(1+cosx\right)\left(1+sinx+sin^2x\right)=\left(1+sinx\right)\left(1+cosx+cos^2x\right)\)
\(\Leftrightarrow sin^2x+sin^2x.cosx=cos^2x+cos^2x.sinx\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx+cosx\right)+sinx.cosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=0\Rightarrow x=\dfrac{\pi}{4}+k\pi\\sinx+cosx+sinx.cosx=0\left(2\right)\end{matrix}\right.\)
Xét (2), đặt \(sinx+cosx=t\Rightarrow\left|t\right|\le\sqrt{2}\)
\(sinx.cosx=\dfrac{t^2-1}{2}\)
Pt (2) trở thành:
\(t+\dfrac{t^2-1}{2}=0\Leftrightarrow t^2+2t-1=0\Rightarrow\left[{}\begin{matrix}t=-1+\sqrt{2}\\t=-1-\sqrt{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{2}-1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}-1}{\sqrt{2}}\)
\(\Rightarrow...\)
Đúng 0
Bình luận (0)
Giải chi tiết giúp mình với

