Trong mặt phẳng với hệ tọa độ OxyCho tamn giác ABC với A(-2;1), B(0;3), C(-1;4)
/ Viết phương trình đường tròn tâm A và đi qua C
Trong mặt phẳng với hệ tọa độ OxyCho tamn giác ABC với A(1;2), B(2;-3), C(3;5)
c) Đường tròn (C) có đường kính BC.
\(\overrightarrow{BC}=\left(1;8\right)\Rightarrow BC=\sqrt{1^2+8^2}=\sqrt{65}\)
Gọi M là trung điểm BC \(\Rightarrow M\left(\dfrac{5}{2};1\right)\)
Đường tròn đường kính BC nhận M là tâm và có bán kính \(R=\dfrac{BC}{2}=\dfrac{\sqrt{65}}{2}\)
Phương trình:
\(\left(x-\dfrac{5}{2}\right)^2+\left(y-1\right)^2=\dfrac{65}{4}\)
Trong mặt phẳng với hệ tọa độ OxyCho tamn giác ABC với A(-2;1), B(0;3), C(-1;4)
/ Viết phương trình tham số của đường thẳng AB
\(\overrightarrow{AB}=\left(2;2\right)=2\left(1;1\right)\)
\(\Rightarrow\) Đường thẳng AB nhận \(\overrightarrow{u}=\left(1;1\right)\) là 1 vtcp
Phương trình AB đi qua \(A\left(-2;1\right)\) và có vtcp (1;1) là:
\(\left\{{}\begin{matrix}x=-2+t\\y=1+t\end{matrix}\right.\)
Trong mặt phẳng O x y cho tam giác ABC có A ( 2 ; 1 ) , B ( - 1 ; 2 ) , C ( 3 ; 0 ) . Tứ giác A B C E là hình bình hành khi tọa độ E là cặp số nào sau đây?
A. ( 6 ; - 1 )
B. ( 0 ; 1 )
C. ( 1 ; 6 )
D. ( 6 ; 1 )
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(-2;4), B(4;1), C(-2;-1). Tìm tọa độ trực tâm H tam giác.
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3 x + 2 y + z + 14 = 0
B. 2 x + y + 3 z + 9 = 0
C. 3 x + 2 y + z - 14 = 0
D. 2 x + y + z - 9 = 0
Đáp án A.
Ta có A M ⊥ B C ⊥ O A ⇒ B C ⊥ O A M ⇒ B C ⊥ O M
Tương tự ta cũng có O M ⊥ A C ⇒ O M ⊥ P ⇒ P (P) nhận O M ¯ = 3 ; 2 ; 1 là vecto pháp tuyến.
Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với O M ¯ và không chứa điểm M thì thỏa.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3x+2y+z+14=0
B. 2x+y+3z+9=0
C. 3x+2y+z-14=0
D. 2x+y+z-9=0.
Chọn A
Gọi A(a;0;0);B(0;b;0);C(0;0;c)
Phương trình mặt phẳng (P) có dạng:
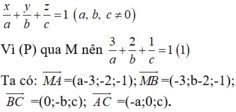
Vì M là trực tâm của tam giác ABC nên:
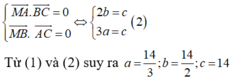
Khi đó phương trình (P): 3x+2y+z-14=0.
Vậy mặt phẳng song song với (P) là: 3x+2y+z+14=0.
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(0;1;2), B(2;-2;0), C(-2;0;1). Mặt phẳng (P) đi qua A, trực tâm H của tam giác ABC và vuông góc với mặt phẳng ( ABC) có phương trình là
A. 4x + 2y - z + 4 = 0
B. 4x + 2y + z - 4 = 0
C. 4x - 2y - z + 4 = 0
D. 4x - 2y + z + 4 = 0
Đáp án C.
Dễ thấy 4.0 - 2.1 - 2 + 4 = 0
![]()
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2;-1), B(4;5) và C(-3;2). Lập phương trình đường cao của tam giác ABC kẻ từ A.
A. 7x + 3y - 11 = 0
B. -3x + 7y + 13 = 0
C. 3x + 7y + 1 = 0
D. 7x + 3y + 13 = 0
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2) 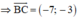
Phương trình đường cao AH đi qua A(2;-1) nhận 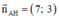 là VTPT là:
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G 2 3 ; 0 , biết M(1;1) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A.(2;0)
B.(-2;0)
C.(0;-2)
D.(0;2)