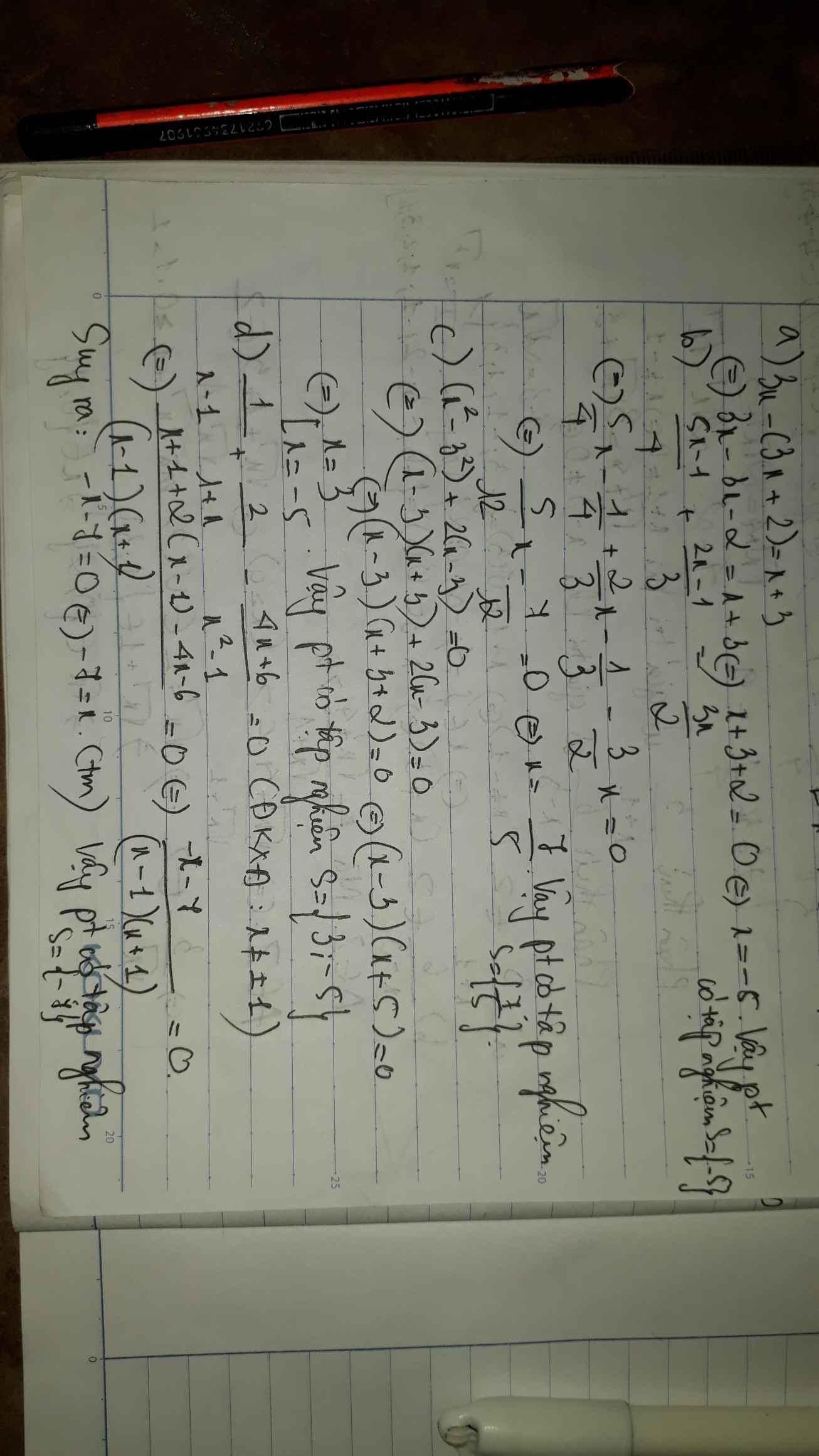giải phương trình 3\(x^2\) . 4\(x+1\) - \(\dfrac{1}{3^x}\) = 0
HP
Những câu hỏi liên quan
Giải phương trình:
\(\dfrac{1}{x}+\dfrac{1}{x+1}+\dfrac{1}{x+2}+\dfrac{1}{x+3}+\dfrac{1}{x+4}=0\)
ĐKXĐ : \(x\notin\left\{0;-1;-2;-3;-4\right\}\)
Ta có \(\dfrac{1}{x}+\dfrac{1}{x+1}+\dfrac{1}{x+2}+\dfrac{1}{x+3}+\dfrac{1}{x+4}=0\)
\(\Leftrightarrow\dfrac{2x+4}{x.\left(x+4\right)}+\dfrac{2x+4}{\left(x+1\right).\left(x+3\right)}+\dfrac{1}{x+2}=0\)
\(\Leftrightarrow\dfrac{2x+4}{\left(x+2\right)^2-4}+\dfrac{2x+4}{\left(x+2\right)^2-1}+\dfrac{1}{x+2}=0\) (*)
Đặt x + 2 = a \(\left(a\ne0\right)\)
(*) \(\Leftrightarrow\dfrac{2a}{a^2-4}+\dfrac{2a}{a^2-1}+\dfrac{1}{a}=0\)
\(\Leftrightarrow\dfrac{2}{a-\dfrac{4}{a}}+\dfrac{2}{a-\dfrac{1}{a}}+\dfrac{1}{a}=0\) (**)
Đặt \(\dfrac{1}{a}=b\left(b\ne0\right)\) \(\Rightarrow ab=1\)
Ta được (**) \(\Leftrightarrow\dfrac{2}{a-4b}+\dfrac{2}{a-b}+b=0\)
\(\Leftrightarrow\dfrac{2b}{1-4b^2}+\dfrac{2b}{1-b^2}+b=0\)
\(\Leftrightarrow\dfrac{2}{1-4b^2}+\dfrac{2}{1-b^2}=-1\)
\(\Rightarrow4-10b^2=-4b^4+5b^2-1\)
\(\Leftrightarrow4b^4-15b^2+5=0\) (***)
Đặt b2 = t > 0
Ta có (***) <=> \(4t^2-15t+5=0\Leftrightarrow t=\dfrac{15\pm\sqrt{145}}{8}\) (tm)
\(\Leftrightarrow b=\pm\sqrt{\dfrac{15\pm\sqrt{145}}{8}}\)
mà x + 2 = a ; ab = 1
nên \(x=\pm\sqrt{\dfrac{8}{15\pm\sqrt{145}}}-2\)
Thử lại ta có phương trình có 4 nghiệm như trên
Đúng 0
Bình luận (0)
bài 1 giải các phương trình sau:h,left(dfrac{3}{4}x-1right)left(dfrac{5}{3}x+2right)0bài 2 giải các phương trình sau:b,3x-152x(x-5) m,(1-x)(5x+3)(3x-7)(x-1)d,x(x+6)-7x-420 p,left(2x-1right)^2-40f,x^3+2x^2-left(x-2right)0 r,left(2x-1right)^249h,(3x-1)(6x+1)(x+7)(3x-1) t,left(5x-3right)^2-left(4x-7right)^20j,left(2x-5right)^2-left(x+2right)^20 u,x^2-10x+160w,x...
Đọc tiếp
bài 1 giải các phương trình sau:
h,\(\left(\dfrac{3}{4}x-1\right)\left(\dfrac{5}{3}x+2\right)=0\)
bài 2 giải các phương trình sau:
b,3x-15=2x(x-5) m,(1-x)(5x+3)=(3x-7)(x-1)
d,x(x+6)-7x-42=0 p,\(\left(2x-1\right)^2-4=0\)
f,\(x^3+2x^2-\left(x-2\right)=0\) r,\(\left(2x-1\right)^2=49\)
h,(3x-1)(6x+1)=(x+7)(3x-1) t,\(\left(5x-3\right)^2-\left(4x-7\right)^2=0\)
j,\(\left(2x-5\right)^2-\left(x+2\right)^2=0\) u,\(x^2-10x+16=0\)
w,\(x^2-x-12=0\)
Bài `1:`
`h)(3/4x-1)(5/3x+2)=0`
`=>[(3/4x-1=0),(5/3x+2=0):}=>[(x=4/3),(x=-6/5):}`
______________
Bài `2:`
`b)3x-15=2x(x-5)`
`<=>3(x-5)-2x(x-5)=0`
`<=>(x-5)(3-2x)=0<=>[(x=5),(x=3/2):}`
`d)x(x+6)-7x-42=0`
`<=>x(x+6)-7(x+6)=0`
`<=>(x+6)(x-7)=0<=>[(x=-6),(x=7):}`
`f)x^3-2x^2-(x-2)=0`
`<=>x^2(x-2)-(x-2)=0`
`<=>(x-2)(x^2-1)=0<=>[(x=2),(x^2=1<=>x=+-2):}`
`h)(3x-1)(6x+1)=(x+7)(3x-1)`
`<=>18x^2+3x-6x-1=3x^2-x+21x-7`
`<=>15x^2-23x+6=0<=>15x^2-5x-18x+6=0`
`<=>(3x-1)(5x-1)=0<=>[(x=1/3),(x=1/5):}`
`j)(2x-5)^2-(x+2)^2=0`
`<=>(2x-5-x-2)(2x-5+x+2)=0`
`<=>(x-7)(3x-3)=0<=>[(x=7),(x=1):}`
`w)x^2-x-12=0`
`<=>x^2-4x+3x-12=0`
`<=>(x-4)(x+3)=0<=>[(x=4),(x=-3):}`
Đúng 1
Bình luận (0)
`m)(1-x)(5x+3)=(3x-7)(x-1)`
`<=>(1-x)(5x+3)+(1-x)(3x-7)=0`
`<=>(1-x)(5x+3+3x-7)=0`
`<=>(1-x)(8x-4)=0<=>[(x=1),(x=1/2):}`
`p)(2x-1)^2-4=0`
`<=>(2x-1-2)(2x-1+2)=0`
`<=>(2x-3)(2x+1)=0<=>[(x=3/2),(x=-1/2):}`
`r)(2x-1)^2=49`
`<=>(2x-1-7)(2x-1+7)=0`
`<=>(2x-8)(2x+6)=0<=>[(x=4),(x=-3):}`
`t)(5x-3)^2-(4x-7)^2=0`
`<=>(5x-3-4x+7)(5x-3+4x-7)=0`
`<=>(x+4)(9x-10)=0<=>[(x=-4),(x=10/9):}`
`u)x^2-10x+16=0`
`<=>x^2-8x-2x+16=0`
`<=>(x-2)(x-8)=0<=>[(x=2),(x=8):}`
Đúng 1
Bình luận (0)
tính đạo hàm
a) \(y=\dfrac{\left(x-2\right)^2}{\left(2x-3\right)\left(x-1\right)}\)
b) \(y=x+3+\dfrac{4}{x+3}\) giải phương trình y'=0
c) \(y=\dfrac{\left(5x-1\right)\left(x+1\right)}{x+2}\) tính y'(-1)
d) \(y=x-2+\dfrac{9}{x-2}\) giải phương trình y'=0
a:
ĐKXĐ: \(x\notin\left\{\dfrac{3}{2};1\right\}\)
\(y=\dfrac{\left(x-2\right)^2}{\left(2x-3\right)\left(x-1\right)}=\dfrac{x^2-4x+4}{2x^2-2x-3x+3}\)
=>\(y=\dfrac{x^2-4x+4}{2x^2-5x+3}\)
=>\(y'=\dfrac{\left(x^2-4x+4\right)'\left(2x^2-5x+3\right)-\left(x^2-4x+4\right)\left(2x^2-5x+3\right)'}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{\left(2x-4\right)\left(2x^2-5x+3\right)-\left(2x-5\right)\left(x^2-4x+4\right)}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{4x^3-10x^2+6x-8x^2+20x-12-2x^3+8x^2-8x+5x^2-20x+20}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{2x^3-5x^2-2x+8}{\left(2x^2-5x+3\right)^2}\)
b:
ĐKXĐ: x<>-3
\(y=\left(x+3\right)+\dfrac{4}{x+3}\)
=>\(y'=\left(x+3+\dfrac{4}{x+3}\right)'=1+\left(\dfrac{4}{x+3}\right)'\)
\(=1+\dfrac{4'\left(x+3\right)-4\left(x+3\right)'}{\left(x+3\right)^2}\)
=>\(y'=1+\dfrac{-4}{\left(x+3\right)^2}=\dfrac{\left(x+3\right)^2-4}{\left(x+3\right)^2}\)
y'=0
=>\(\left(x+3\right)^2-4=0\)
=>\(\left(x+3+2\right)\left(x+3-2\right)=0\)
=>(x+5)(x+1)=0
=>x=-5 hoặc x=-1
c:
ĐKXĐ: x<>-2
\(y=\dfrac{\left(5x-1\right)\left(x+1\right)}{x+2}\)
=>\(y=\dfrac{5x^2+5x-x-1}{x+2}=\dfrac{5x^2+4x-1}{x+2}\)
=>\(y'=\dfrac{\left(5x^2+4x-1\right)'\left(x+2\right)-\left(5x^2+4x-1\right)\left(x+2\right)'}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{\left(5x+4\right)\left(x+2\right)-\left(5x^2+4x-1\right)}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{5x^2+10x+4x+8-5x^2-4x+1}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{10x+9}{\left(x+2\right)^2}\)
\(y'\left(-1\right)=\dfrac{10\cdot\left(-1\right)+9}{\left(-1+2\right)^2}=\dfrac{-1}{1}=-1\)
d:
ĐKXĐ: x<>2
\(y=x-2+\dfrac{9}{x-2}\)
=>\(y'=\left(x-2+\dfrac{9}{x-2}\right)'=1+\left(\dfrac{9}{x-2}\right)'\)
\(=1+\dfrac{9'\left(x-2\right)-9\left(x-2\right)'}{\left(x-2\right)^2}\)
=>\(y'=1+\dfrac{-9}{\left(x-2\right)^2}=\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}\)
y'=0
=>\(\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}=0\)
=>\(\left(x-2\right)^2-9=0\)
=>(x-2-3)(x-2+3)=0
=>(x-5)(x+1)=0
=>x=5 hoặc x=-1
Đúng 1
Bình luận (0)
Giải các phương trình
1,\(3x-1=0\\\) 4, \(\dfrac{x}{3}-\dfrac{x}{5}=4\)
2, \(2-x=3x+1\) 5, \(\dfrac{x-1}{4}+\dfrac{2x+1}{6}=\dfrac{3}{2}\)
3, \(2\left(x-2\right)-1=5x\)
1,\(3x-1=0\Leftrightarrow3x=-1\Leftrightarrow x=-\dfrac{1}{3}\)
2,\(2-x=3x+1\Leftrightarrow2-1=3x+x\rightarrow1=4x\Rightarrow x=-\dfrac{1}{4}\)
Đúng 1
Bình luận (0)
3,\(2\left(x-2\right)-1=5x\Leftrightarrow2x-4-1=5x\Leftrightarrow2x-5x=4+1\Rightarrow3x=5\Rightarrow x=\dfrac{5}{3}\)
4,\(\dfrac{x}{3}-\dfrac{x}{5}=4\Leftrightarrow\dfrac{5x}{15}-\dfrac{3x}{15}=\dfrac{60}{15}\Rightarrow5x-3x=60\Rightarrow2x=60\Rightarrow x=\dfrac{60}{2}=30\)
Đúng 1
Bình luận (0)
5,\(\dfrac{x-1}{4}+\dfrac{2x+1}{6}=\dfrac{3}{2}\Leftrightarrow\dfrac{3\left(x-1\right)}{12}+\dfrac{2\left(2x+1\right)}{12}=\dfrac{18}{12}\)
\(3\left(x-1\right)+2\left(2x+1\right)=18\Leftrightarrow3x-3+4x+2=18\Leftrightarrow3x+4x=3-2+18\Rightarrow7x=19\Rightarrow x=\dfrac{19}{2}\)
Đúng 1
Bình luận (0)
giải các phương trình sau
a, 3(x-1) -3=2(x+3)
b, \(\dfrac{x+4}{4}-\dfrac{x+3}{3}=\dfrac{x+6}{6}\)
c,\(\left(2x-1\right)^2-x^2=0\)
d,\(\dfrac{x}{x+3}-\dfrac{2x}{x-3}-\dfrac{3x}{9-x^2}=0\)
d: Ta có: \(\dfrac{x}{x+3}-\dfrac{2x}{x-3}-\dfrac{3x}{9-x^2}=0\)
\(\Leftrightarrow x^2-3x-2x^2-6x+3x=0\)
\(\Leftrightarrow-x^2-6x=0\)
\(\Leftrightarrow-x\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-6\left(nhận\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
a: Ta có: \(3\left(x-1\right)-3=2\left(x+3\right)\)
\(\Leftrightarrow3x-3-3=2x+6\)
\(\Leftrightarrow x=12\)
b: Ta có: \(\dfrac{x+4}{4}-\dfrac{x+3}{3}=\dfrac{x+6}{6}\)
\(\Leftrightarrow3x+12-4x-12=2x+12\)
\(\Leftrightarrow-3x=12\)
hay x=-4
c: Ta có: \(\left(2x-1\right)^2-x^2=0\)
\(\Leftrightarrow\left(x-1\right)\left(3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
1) Giải phương trình: $2 x^{2}+3 x-5=0$.
2) Giải hệ phương trình: $\left\{\begin{array}{l}x+2 y=1 \\ -3 x+4 y=-18\end{array}\right.$
3) Rút gọn biểu thức: $P=\left(\dfrac{1}{x+\sqrt{x}}-\dfrac{1}{\sqrt{x}+1}\right): \dfrac{\sqrt{x}}{x+2 \sqrt{x}+1}$ với $x>0$.
\(2x^2+3x-5=0\)
\(< =>2x^2-2x+5x-5=0\)
\(< =>2x\left(x-1\right)+5\left(x-1\right)=0\)
\(< =>\left(x-1\right)\left(2x+5\right)=0\)
\(< =>\orbr{\begin{cases}x=1\\x=-\frac{5}{2}\end{cases}}\)
\(\hept{\begin{cases}x+2y=1\\-3x+4y=-18\end{cases}}\)
\(< =>\hept{\begin{cases}-3x-6y=-3\\-3x-6y+10y=-18\end{cases}}\)
\(< =>\hept{\begin{cases}x+2y=1\\10y=-18+3=-15\end{cases}}\)
\(< =>\hept{\begin{cases}x+2y=1\\y=-\frac{3}{2}\end{cases}< =>\hept{\begin{cases}x-3=1\\y=-\frac{3}{2}\end{cases}< =>\hept{\begin{cases}x=4\\y=-\frac{3}{2}\end{cases}}}}\)
Bài 1 : Ta có : \(\Delta=9-4\left(-5\right).2=9+40=49>0\)
\(x_1=\frac{-3-7}{4}=-\frac{11}{4};x_2=\frac{-3+7}{4}=1\)
Bài 2 :
\(\hept{\begin{cases}x+2y=1\\-3x+4y=-18\end{cases}\Leftrightarrow\hept{\begin{cases}2x+4y=2\\-3x+4y=-18\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}5x=20\\x+2y=1\end{cases}\Leftrightarrow\hept{\begin{cases}x=4\\y=-\frac{3}{2}\end{cases}}}\)
Vậy hệ pt có một nghiệm ( x ; y ) = ( 4 ; -3/2 )
Xem thêm câu trả lời
Giải các phương trình, bất phương trình sau:
1) \(\sqrt{3x+7}-5< 0\)
2) \(\sqrt{-2x-1}-3>0\)
3) \(\dfrac{\sqrt{3x-2}}{6}-3=0\)
4) \(-5\sqrt{-x-2}-1< 0\)
5) \(-\dfrac{2}{3}\sqrt{-3-x}-3>0\)
1) \(\sqrt[]{3x+7}-5< 0\)
\(\Leftrightarrow\sqrt[]{3x+7}< 5\)
\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)
\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)
\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)
Đúng 0
Bình luận (0)
1) GIẢI phương trình :
a) 2x-6=0
b) x2-4x=0
c)\(\dfrac{x+2}{x-3}\)-\(\dfrac{3}{x}\)=\(\dfrac{x+9}{x^2-3x}\)
d) \(\dfrac{x-1}{2}\)-\(\dfrac{x-2}{3}\)=x-\(\dfrac{x-3}{4}\)
giải chi tiết giúp mik ah
a) \(2x-6=0\)
\(\Leftrightarrow2x=6\)
\(\Leftrightarrow x=\dfrac{6}{2}=3\)
b) \(x^2-4x=0\)
\(\Leftrightarrow x\left(x-4\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
Đúng 2
Bình luận (1)
giải các phương trình sau
a, 3x -(3x+2) =x+3
b, \(\dfrac{5x-1}{4}+\dfrac{2x-1}{3}=\dfrac{3x}{2}\)
c, \(\left(x^2-3^2\right)+2\left(x-3\right)=0\)
d,\(\dfrac{1}{x-1}+\dfrac{2}{1+x}-\dfrac{4x+6}{x^2-1}=0\)
a: Ta có: \(3x-\left(3x+2\right)=x+3\)
\(\Leftrightarrow x+3=-2\)
hay x=-5
b: Ta có: \(\dfrac{5x-1}{4}+\dfrac{2x-1}{3}=\dfrac{3x}{2}\)
\(\Leftrightarrow15x-3+8x-4=18x\)
\(\Leftrightarrow5x=7\)
hay \(x=\dfrac{7}{5}\)
Đúng 0
Bình luận (0)