Chứng minh rằng AB vuông góc với CD khi và chỉ khi AC2 - AD2 = BC2 - BD2
VM
Những câu hỏi liên quan
Cho tứ diện ABCD. Chứng minh rằng AB vuông góc với CD khi và chỉ khi A C 2 + B D 2 = A D 2 + B C 2
Giả sử AB ⊥ CD ta phải chứng minh:
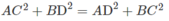
Thật vậy, kẻ BE ⊥ CD tại E, do AB⊥CD ta suy ra CD ⊥ (ABE) nên CD ⊥ AE. Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:
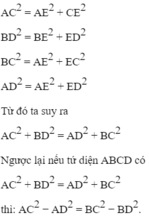
Nếu
A
C
2
−
A
D
2
=
B
C
2
−
B
D
2
=
k
2
thì trong mặt phẳng (ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho 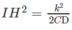
Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên. Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD ⊥ AB.
Nếu A C 2 − A D 2 = B C 2 − B D 2 = - k 2 thì ta có và đưa về trường hợp xét như trên A C 2 − A D 2 = B C 2 − B D 2 = - k 2 .
Chú ý. Từ kết quả của bài toán trên ta suy ra:
Tứ diện ABCD có các cặp cạnh đối diện vuông góc với nhau khi và chỉ khi A B 2 + C D 2 = A C 2 + B C 2 .
Đúng 0
Bình luận (0)
Cho tam giác cân ABC (AB = AC), đường cao CD (D ở giữa A và B).
Chứng minh rằng: AB2 + BC2 + AC2 = BD2 + 2AD2 + 3DC2
Cho hình thang ABCD (AB song song DC), chân các đường vuông góc kẻ từ A, B xg DC nằm trên cạnh DC. C/m rg: AC2 + BD2 = AD2 + BC2 + 2AB.DC.
Cho mặt cầu tâm O bán kính r. Gọi (
α
) là mặt phẳng cách tâm O một khoảng h (0 h r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng (
α
) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Chứng minh các tổng
AD
2
+
BC
2
và...
Đọc tiếp
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Chứng minh các tổng AD 2 + BC 2 và AC 2 + BD 2 có giá trị không đổi
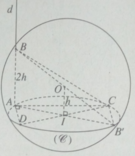
Tam giác ADC vuông tại A nên AD 2 = DC 2 - AC 2 (1)
Tam giác ABC vuông tại A nên BC 2 = AC 2 + AB 2 (2)
Từ (1) và (2) ta suy ra AD 2 + BC 2 = DC 2 + AB 2 (3)
Ta lại có:
AC 2 = DC 2 - AD 2 và BD 2 = AD 2 + AB 2 (4)
DC 2 = 4 r 2 - h 2 , AB 2 = 4 h 2 (5)
Từ (4) và (5) ta có:
AC 2 + BD 2 = DC 2 + AB 2 = 4 r 2 - h 2 + 4 h 2 = 4 r 2 (6)
Từ (3) và (6) ta có: AD 2 + BC 2 = AC 2 + BD 2 (không đổi)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có trọng tâm G. Chứng minh AB2 + AC2 + AD2 + BC2 + BD2 + CD2 = 4(GA2 + GB2 + GC2 + GD2)
Cho 4 điểm A, B, C, D thỏa mãn hệ thức AC2 + BD2 AD2 + BC2. Tìm mệnh đề đúng? A. AC và AD vuông góc với nhau B. AC và BD vuông góc với nhau C. AB và CD vuông góc với nhau D. AB và BC vuông góc với nhau
Đọc tiếp
Cho 4 điểm A, B, C, D thỏa mãn hệ thức AC2 + BD2 = AD2 + BC2. Tìm mệnh đề đúng?
A. AC và AD vuông góc với nhau
B. AC và BD vuông góc với nhau
C. AB và CD vuông góc với nhau
D. AB và BC vuông góc với nhau
Chọn C
Theo đầu bài ta có: AC2 + BD2 = AD2 + BC2 nên AC2 - AD2 = BC2 - BD2
Suy ra:
![]()
Hay
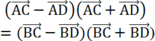
Tương đương
![]()
![]()
![]()
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có hai đường chéo AC vuông góc với BD. Chứng minh rằng:
AB2 + CD2 = AD2 + BC2
Cho hình thang ABCD(AB//CD) có góc ACD=góc BDC.Chứng minh BD2-BC2=AB.CD.
Cho hình thang ABCD(AB//CD) có góc ACD=góc BDC.Chứng minh BD2-BC2=AB.CD
Kẻ 2 đường cao AE, BF
Gọi G là giao điểm 2 đường chéo
\(\widehat{ACD}=\widehat{BDC}\Rightarrow\Delta GCD\) cân tại G \(\Rightarrow GC=GD\) (1)
\(\left\{{}\begin{matrix}\widehat{ACD}=\widehat{BAC}\left(slt\right)\\\widehat{BDC}=\widehat{ABD}\left(slt\right)\\\widehat{ACD}=\widehat{BDC}\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\widehat{BAC}=\widehat{ABD}\) \(\Rightarrow\Delta GAB\) cân tại G \(\Rightarrow GA=GB\) (2)
(1); (2) \(\Rightarrow AC=BD\Rightarrow ABCD\) là hình thang cân
\(\Rightarrow\left\{{}\begin{matrix}AB=EF\\DE=CF\end{matrix}\right.\)
Áp dụng định lý Pitago: \(\left\{{}\begin{matrix}BD^2=DF^2+BF^2\\BC^2=BF^2+CF^2\end{matrix}\right.\)
\(\Rightarrow BD^2-BC^2=DF^2-CF^2=\left(DF+CF\right)\left(DF-CF\right)=CD.EF=CD.AB\) (đpcm)
Đúng 0
Bình luận (0)
Hôm nay 20/11 nma e vẫn phải làm bài tập:((, mn giúp em với hic
Cho hình bình hành ABCD. Chứng minh rầng: AC2 +BD2=2(AB2+AD2)


