Vẽ giùm em câu a với ạ em cảm ơn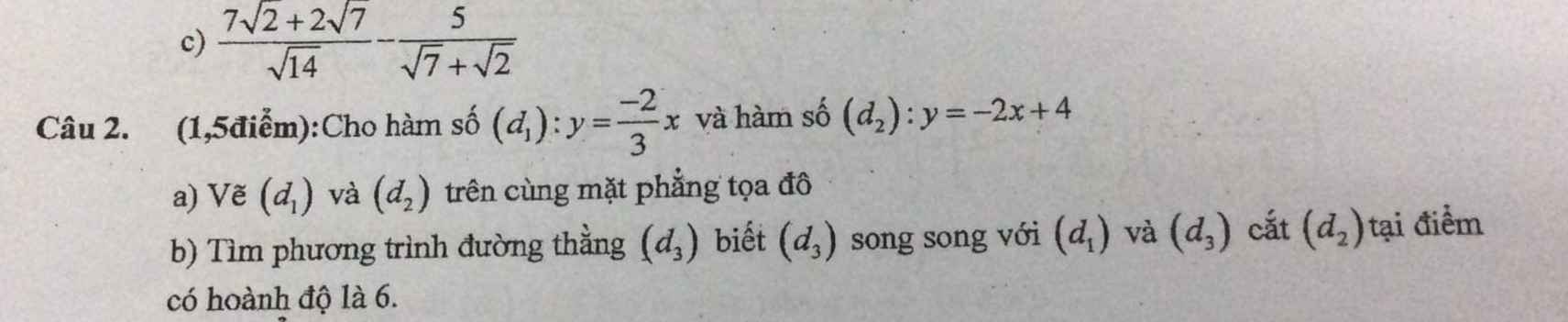
DD
Những câu hỏi liên quan
Vẽ giùm em câu a thôi ạ em cảm ơn 
b) Gọi (d3): y=ax+b
Vì (d3)//(d1) nên \(a=-\dfrac{2}{3}\)
Vậy: (d3): \(y=\dfrac{-2}{3}x+b\)
Thay x=6 vào (d2), ta được:
\(y=-2\cdot6+4=-12+4=-8\)
Thay x=6 và y=-8 vào (d3), ta được:
\(\dfrac{-2}{3}\cdot6+b=-8\)
\(\Leftrightarrow b=-4\)
Vậy: (d3): \(y=\dfrac{-2}{3}x-4\)
Đúng 0
Bình luận (0)
Giúp em câu 2 ạ câu 2 a vẽ phụ em giùm luôn ạ cảm ơn mọi người nhiều
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-2x-3=-\dfrac{1}{2}x+3\\y=-2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{3}{2}x=6\\y=-2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=8-3=5\end{matrix}\right.\)
Đúng 1
Bình luận (0)
vẽ giùm em với ạ em cảm ơn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
Xem chi tiết
Vẽ giùm em sơ đồ tư duy bài 29 phần 1 lớn với ạ em cảm ơn nhìu 😋😋
Mong mn giúp em ạ!
Dạ mn coi các đáp án trong đề nếu có sai mong mn sửa lại đáp án đúng giùm em với có mấy câu em không biết cũng mong mn chỉ giùm EM CẢM ƠN MN TRƯỚC Ạ!
1.A
2.B
3.B
4.C
5.C
6.D
7.A
8.D
9.B
10.B
11.B
12.C
13.B
14.B
15.B
Đúng 3
Bình luận (1)
Giúp em với ạ vẽ hình nữa làm mình câu a) cũng được ạ em cảm ơn nhìu ::)>>33
a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)
Đúng 2
Bình luận (0)
Giúp em với ạ vẽ phụ em câu ạ nữa nha cảm ơn ạ