Cho tứ giác ABCD
a, Chứng minh rằng ; góc BAD + góc ABC + góc BCD + góc COA = 360
b, AC cắt BD tại O Chứng minh rằng
AB + BC + CD + DA < 2 ( AC + BD )
Vẽ hình giùm mình với giải chi tiết nha
: Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của các cạnh AC, AB, BC. *Chứng minh rằng: Tứ giác BNMC là hình thang. *Chứng minh rằng: tứ giác MNEC là hình bình hành. *Chứng minh rằng: Tứ giác AMEN là hình chữ
a: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của AB
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
hay BMNC là hình thang
cho tam giác ABC cân tại A : M là trung điểm AB
N là trung điểm AC
a) cho BC=10cm tính MN
b) chứng minh rằng: tứ giác BNMC là hình thang
c) chứng minh rằng: tứ giác BNMC là hình thang cân
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
a)Vì M là trung điểm của AB, N là trung điểm của AC=>MN là đường trung bình của tam ΔABC=>MN=1/2 BC mà BC = 10cm nên MN = 5cm
b)Vì MN là đường trung bình của tam ΔABC=>MN//BC=> Tứ giác BMNC là hình thang
c)Theo đề bài ta có ΔABC cân tại A => Góc B=C => Tứ giác BMNC là hình thang cân
Cho tứ giác ABCD \(AB=BC=AD\) , và\(\widehat{DAB}\) + \(\widehat{BCD}\) = \(^{^{ }180^o}\)
a) Chứng minh rằng DB là tia phân giác của góc \(\widehat{ADC}\) ?
b) Chứng minh rằng tứ giác ABCD là hình thang cân ?

a. Ta có: AD = AB
=> \(\Delta ABD\) là tam giác cân
=> Góc ADB = góc ABD (1)
Mà góc ABD = góc BDC (so le trong) (2)
Từ (1) và (2), suy ra:
BD là tia phân giác của góc ADC
b. Nối AC
Xét 2 tam giác ABC và ABD có:
AD = BC (gt)
AB chung
=> \(\Delta ABD\sim\Delta ABC\) (1)
Ta có: AD = AB = BC (2)
Từ (1) và (2), suy ra: \(\Delta ABD=\Delta ABC\)
=> Góc A = góc B
Ta có: AB//CD
=> Góc D + góc A = 90o (2 góc trong cùng phía)
Mà góc A = góc B
=> Góc C = góc D
=> ABCD là hình thang cân
Nhưng bậy giờ bn chỉ cần chứng minh đó là hình thang là đc
Bài 1: Cho tứ giác ABCD
a. Có bao nhiêu vectơ khác 0 được thiết lập từ các điểm A, B, C, D.
b. Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. CMR: MQ = NP
Bài 2: Cho tứ giác ABCD. CMR: Tứ giác đó là hình bình hành khi và chỉ khi AB = DC
Giúp mình gấp với ạ :((
Chứng minh rằng trong tứ giác tổng 2 đường chéo lớn hơn tổng hai cạnh đối
Cho tứ giác có AB =BC , góc A + góc C = 180 độ . Chứng minh rằng BD là tia phân giác của Tam giác ADC
a, Gọi AC giao BD tai O
TAm giác OAB có
OA + OB > AB (1)
Tam giác OCD có
OC + OD > CD (2)
cộng vế với vế của (1) và (2) -=> AC + BD > AB + CD
Mình cũng đồng ý với ý kiến của bạn
đúng nhưng bạn thiếu rồi
còn AC+BD>AD+BC nữa
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi 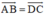
Cho hình chữ nhật abcd.gọi M,N,K lần lượt là trung diểm AH,BH,CD trong đó H là hình chiếu vuông góc của B lên AC
1 chứng minh rằng tứ giác MNCK là hình bình hành.
2 chứng minh rằng N là trực tâm tam giác BCM.
3 chứng minh rằng tứ giác BMKC nội tiếp
4 Đường tròn nội tiếp tứ giác BMKC cắt AB tại I( I khác B ).Chứng mình rằng 2AI^2=AM.AC
Cho hình bình hành ABCD, Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho ![]()
a, Chứng minh rằng: ![]() .
.
b, Chứng minh tứ giác AMCN là hình bình hành.
c, Chứng minh tứ giác BMDN là hình bình hành
Bài 1:
cho tam giác ABC cân tại A các đường cao BE vàCF chứng minh rằng tứ giác BFEC là hình thang cân ?
Bài 2 :
Chứng minh rằng : tứ giác ABCD có góc D = góc C và AD = BC thì tứ giác đí là hònh thang cân ?
bài 1 mk đã giải cho bạn kiên trần cách giải bài đó cũng như bài này nên bạn xem chỗ bạn kiên trần nhé!
bài 2 theo mk là làm như thế này !
à mà bạn tự vẽ hình nhé!!!
Trong tứ giác ABCD , từ đỉnh A kẻ AH \(\perp\)DC , từ đỉnh B kẻ BG \(\perp\)DC.
Xét \(\Delta\)vuông ADH và \(\Delta\) vuông BCG có:
AD = BC ( đề cho)
góc D = góc C ( đề cho )
=> \(\Delta\)vuông ADH = \(\Delta\)vuông BCG ( cạnh huyền - góc nhọn )
=> AH = BG
mặt khác AH // BG ( cùng \(\perp\) BC )
=> Tứ giác ABGH là hình bình hành
=> AB // HG hay AB // DC
Tứ giác ABCD có góc D = góc C và AB // DC
=> ABCD là hình thang cân ( đpcm)
Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\)). Gọi \(M\), \(N\), \(E\) lần lượt là trung điểm của \(AB\), \(AC\), \(BC\)
a) Chứng minh rằng tứ giác \(ANEB\) là hình thang vuông
b) Chứng minh rằng tứ giác \(ANEM\) là hình chữ nhật
c) Qua \(M\) kẻ đường thẳng song song với \(BN\) cắt \(EN\) tại \(F\). Chứng minh rằng tứ giác \(AFCE\) là hình thoi
d) Gọi \(D\) là điểm đối cứng của \(E\) qua \(M\). Chứng minh rằng \(A\) là trung điểm của \(DF\)
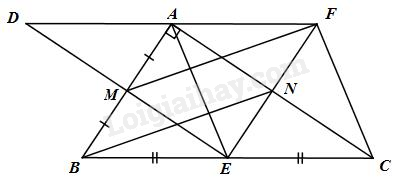
a) \(N\), \(E\) lần lượt là trung điểm của \(AC\) và \(BC(gt)\); Suy ra \(NE\) là đường trung bình của tam giác \(ABC\).
Suy ra \(NE\) // \(AB\)
Suy ra tứ giác \(ANEB\) là hình thang.
Mà \(\widehat {NAB} = 90^\circ \) (do \(\Delta ABC\) vuông tại \(A\))
Do đó tứ giác \(ANEB\) là hình thang vuông.
b) \(M\), \(E\) lần lượt là trung điểm của \(AB\) và \(BC\) (gt);
Suy ra \(ME\) là đường trung bình của \(\Delta ABC\)
Suy ra \(ME\) // \(AC\) hay \(ME\) // \(AN\)
Mà \(AM\) // \(NE\) (do \(AB\) // \(NE\))
Suy ra tứ giác \(AMEN\) là hình bình hành
Mà \(\widehat {{\rm{MAN}}} = 90^\circ \) nên \(AMEN\) là hình chữ nhật
c) Xét tứ giác \(BMFN\) có: \(MF\) // \(BN\) (gt) và \(BM\) // \(FN\) (do \(AB\) // \(NE\))
Suy ra \(BMFN\) là hình bình hành
Suy ra \(BM = FN\)
Mặt khác \(NE = AM\) (Tứ giác \(ANEM\) là hình chữ nhật) và \(AM = BM\)
Suy ra \(FN = NE\)
Tứ giác \(AFCE\) có \(N\) là trung điểm của \(AC\) và \(EF\)
Suy ra \(AFCE\) là hình bình hành
Mà \(AC \bot EF\)
Do đó \(AFCE\) là hình thoi
d) Xét tứ giác \(ADBE\) ta có: \(DE\) và \(AB\) cắt nhau tại \(M\) (gt)
Mà \(M\) là trung điểm của \(AB\) (gt)
\(M\) là trung điểm của \(DE\) (do \(D\) đối xứng với \(E\) qua \(M\))
Suy ra \(ADBE\) là hình bình hành
Suy ra \(AD\) // \(BE\) hay \(AD\) // \(EC\)
Mà \(AF\) // \(EC\) (do \(AECF\) là hình thoi)
Suy ra \(A,D,F\) thẳng hàng (1)
Mà \(ADBE\) là hình bình hành
Suy ra \(BE\) // \(AD\)
Mà \(AF = EC\) (do \(AFCE\) là hình thoi); \(EB = EC\) (gt)
Suy ra \(AD = AF\)(2)
Từ (1) và (2) suy ra \(A\) là trung điểm của \(DF\)