Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC, biết AB=13cm, AH=12cm, HC=16cm
Tính AC, BC
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC. Cho biết AB = 13cm, AH = 12cm, HC = 16cm. Tính độ dài AC, BC.
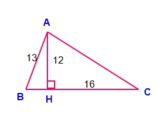
Áp dụng định lí Pi-ta-go trong ΔAHC vuông tại H ta có:
AC2 = AH2 + HC2 = 122 + 162 = 144 + 256 = 400
⇒ AC = 20 (cm)
Áp dụng định lí Pi-ta-go trong ΔAHB vuông tại H ta có:
BH2 + AH2 = AB2 ⇒ BH2 = AB2 - AH2 = 132 - 122 = 169 -144 = 25
⇒ BH = 5cm
Do đó BC = BH + HC = 5 + 16 = 21 (cm)
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC (H thuộc BC). Biết AB = 13cm, AH=12cm,HC =16cm . Tính AC,BC
tam giác AHB vuông tại H có: BH2=AB2-AH2=132-122=25( ĐL Pytago) => BH=5 cm
BC=BH+HC=5+16=21 cm
Tam giác AHC vuông tại H có: AH2+ HC2=AC2( đl Pytago) --> AC2=122+ 162=20 cm
Tam giác AHB vuông tại H có: AB2= AH2+BH2( đli Pytago) => BH2=AB2-AH2=132- 122=25 -> BH=5 cm
BC= BH+HC=5+16=21 cm
Tam giác AHC vuông tại H có: AC2= AH2+HC2( đli Pytago) => AC2= 122+ 162=400 --> AC= 20 cm
Áp dụng Py-ta-go vào \(\Delta\) vuông AHC ta có:
AC2 = AH2 + HC2
hay AC2 = 122 + 162
=> AC2 = 400
=> AC = 20 cm
Áp dụng Py-ta-go vào \(\Delta\) vuông AHC ta có:
AB2 = AH2 + BH2
hay 132 = 122 + BH2
=> BH2 = 132 - 122
=> BH2 = 25
=> BH = 5 cm
Có BC = BH + HC
hay BC = 5 + 16 = 21
Vậy AC = 20 cm và BC = 21cm
XONG !!![]()
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC (H thuộc BC). Biết AB=13cm,AH=12cm,HC=16cm. Tính AC,BC
Xét tam giác AHC có góc AHC=90
=>Tam giác AHC vuông tai H
Áp dụng định lí Py ta go cho tam giác AHC , ta có
AH^2+HC^2=AC^2
=>12^2+16^2=AC^2
=>400=AC^2
=>AC=20(cm)
Áp dụng định lí Py ta go cho tam giác AHB , ta có
AH^2+HB^2=AB^2
=>12^2+HB^2=13^2
=>HB^2=25
=>HB=5(cm)
Ta có BH+HC=BC
=>5+16=BC
=>BC=21 (cm)
Vậy AC=20cm ; BC=21cm
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+16^2=400\)
hay AC=20(cm)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow HB^2=AB^2-AH^2=13^2-12^2=25\)
hay HB=5(cm)
Ta có: HB+HC=BC(H nằm giữa B và C)
nên BC=5+16=21(cm)
Vậy: AC=20cm; BC=21cm
AH \(\perp\) BC ( gt )
\(\Rightarrow\) Tam giác HAC vuông tại H
\(\Rightarrow\) \(^{AC^2}\) = \(^{AH^2}\) + \(^{HC^2}\)
\(\Rightarrow\) \(^{AC^2}\)= \(^{12^2}\) + \(^{16^2}\)
\(\Rightarrow\) \(^{AC^2}\)= 144 + 256
\(\Rightarrow\) \(^{AC^2}\)= 400
\(\Rightarrow\) AC = 20 ( cm )
AH \(\perp\) BC ( gt )
\(\Rightarrow\) Tam giác HAB vuông tại H
\(\Rightarrow\) \(AB^2\) = \(AH^2\) + \(BH^2\)
\(\Rightarrow\) \(BH^2\) = \(AB^2\) - \(AH^2\)
\(\Rightarrow\) \(BH^2\) = \(13^2\) - \(12^2\)
\(\Rightarrow\) \(BH^2\) = 169 - 144
\(\Rightarrow\) \(BH^2\) = 25
\(\Rightarrow\) BH = 5 ( cm )
Có: BH + HC = BC ( Vì H nằm giữa B và C )
\(\Rightarrow\) 5 + 16 = 21 ( cm )
Vậy AC = 20 cm
BC = 21 cm
Học tốt
Cho tam giác ABC nhọn. Kẻ AH vuông góc với BC tại H. Biết rằng AB =13cm,AH = 12cm, HC = 16cm. Tính độ dài các cạnh AC, BC.
CHo tam giác ABC nhọn, kẻ AH vuông góc với BC (H thuộc BC). Biết AB=13cm, AH=12cm, HC=16cm. Tính AC, BC
Ta có : AC^2=AH^2+HC^2 (định lí Pytago trong tam giác vuông ACH) AC^2=12^2+16^2 AC^2=144+256 AC^2=400 AC=Căn 400=20(cm) Ta có : AB^2=AH^2+HB^2 (định lí Pytago trong tam giác vuông ABH) 13^2=12^2+HB^2 169=144+HB^2 HB^2=169-144 HB^2=25 HB=Căn 25=5(cm) Ta có : BC=HB+HC BC=5+16 BC=21(cm)
áp dụng pitago tính đc BH cộng đoạn thẳng tính đc BC,áp dụng pitago tính đc AC
cho tam giác nhọn ABC . kẻ AH vuông góc với BC ( H thuộc BC ) . biết AB =13cm , AH=12cm và HC=16cm . tính chu vi tam giác ABC
Trả lời :
Bạn vào câu hỏi tương tự hoặc lên mạng kham khải bài nhá.
# chúc bạn học tốt ạ #
20 cm nha !
nhớ link nhé!
Vì tam giác ABC là tam giác nhọn :
=> AB = AC = ( 13 cm )
HB = HC = ( 16 cm )
=> Chu vi tam giác ABH là :
13 + 12 + 16 = 41 ( cm )
=> Chu vi tam giác AHC là :
13 + 12 + 16 = 41 ( cm )
=> Tam giác ABC là :
41 + 41 = 82 ( cm )
Vậy :....................
p/s : Ngu toán hình nên kh chắc ạ ^^
Bài 1. cho Tam giác Abc nhọn , kẻ AH vuông góc với BC(H thuộc BC)
AB=13cm;AH=12cm;HC=16cm. Tính AC . Tính BC