Giúp mình giải tìm giá trị nhỏ nhất và lớn nhất của hàm số y=5 cos căn x+pi /4
PT
Những câu hỏi liên quan
Giúp mình giải tìm giá trin lớn nhất và nhỏ nhất của hàm số y=cos pi x trên đoạn [1/4;3/2]
\(x\in\left[\dfrac{1}{4};\dfrac{3}{2}\right]\Rightarrow\pi x\in\left[\dfrac{\pi}{4};\dfrac{3\pi}{2}\right]\)
\(\Rightarrow cos\left(\pi x\right)\in\left[-1;\dfrac{\sqrt{2}}{2}\right]\)
\(y_{max}=\dfrac{\sqrt{2}}{2}\) khi \(x=\dfrac{1}{4}\)
\(y_{min}=-1\) khi \(x=1\)
Đúng 2
Bình luận (0)
Giúp mik giải tìm giá trị nhỏ nhất và lớn nhất của hàm số y= căn 4-3 cos^2 3x +1
Đề là:
\(y=\sqrt{4-3cos^23x}+1\) đúng không nhỉ?
Ta có:
\(0\le cos^23x\le1\Rightarrow1\le\sqrt{4-3cos^23x}\le2\)
\(\Rightarrow2\le y\le3\)
\(y_{min}=2\) khi \(cos^23x=1\)
\(y_{max}=3\) khi \(cos3x=0\)
Đúng 2
Bình luận (0)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) \(y=f\left(x\right)=\dfrac{4}{\sqrt{5-2\cos^2x\sin^2x}}\)
b)\(y=f\left(x\right)=3\sin^2x+5\cos^2x-4\cos2x-2\)
c)\(y=f\left(x\right)=\sin^6x+\cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) y=f(x)=\(\dfrac{4}{\sqrt{5-2cos^2xsin^2x}}\)
b)y=f(x)=\(3sin^2x+5cos^2x-4cos2x-2\)
c)y=f(x)=\(sin^6x+cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:1,y5-3cosx2,y3cos^2x-2cosx+23,ycos^2x+2cos2x4,ysqrt{5-2sin^2x.cos^2x}5,ycos2x-cosleft(2x-dfrac{pi}{3}right)6,ysqrt{3}sinx-cosx-27,y2cos^2x-sin2x+58,y2sin^2x-sin2x+109,ysin^6x+cos^6x
Đọc tiếp
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
1,\(y=5-3cosx\)
2,\(y=3cos^2x-2cosx+2\)
3,\(y=cos^2x+2cos2x\)
4,\(y=\sqrt{5-2sin^2x.cos^2x}\)
5,\(y=cos2x-cos\left(2x-\dfrac{\pi}{3}\right)\)
6,\(y=\sqrt{3}sinx-cosx-2\)
7,\(y=2cos^2x-sin2x+5\)
8,\(y=2sin^2x-sin2x+10\)
9,\(y=sin^6x+cos^6x\)
Giúp mik giải tìm giá trị nhỏ nhất và lớn nhất của hàm số y=2 căn 1-sinx +3
\(Tacó:2\sqrt{1-sinx}+3\ge2.0+3=3\\ dấubằngxảyrakhi\sqrt{1-sinx}=0\Leftrightarrow sinx=1\\ lạicó:sinx\ge-1\Rightarrow\sqrt{1-sinx}\le\sqrt{1-\left(-1\right)}=\sqrt{2}\\ \Rightarrow2\sqrt{1-sinx}+3\le2\sqrt{2}+3\\ \)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số y = cos x + cos x - π 3
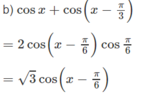
Vậy giá trị nhỏ nhất của y là -√3 đạt được chẳng hạn, tại x = 7π/6; giá trị lớn nhất của y là √3, đạt được chẳng hạn tại x = π/6
Đúng 0
Bình luận (0)
Giúp mik nhanh với tìm giá trị lớn nhất và nhỏ nhất của hs y=-1-cos^2(2x+pi/3)
\(y=-1-cos^2\left(2x+\dfrac{\pi}{3}\right)\)
\(=-\dfrac{3}{2}+\dfrac{1}{2}-cos^2\left(2x+\dfrac{\pi}{3}\right)\)
\(=-\dfrac{3}{2}-\dfrac{1}{2}\left[2cos^2\left(2x+\dfrac{\pi}{3}\right)-1\right]\)
\(=-\dfrac{3}{2}-\dfrac{1}{2}cos\left(4x+\dfrac{2\pi}{3}\right)\)
Vì \(cos\left(4x+\dfrac{2\pi}{3}\right)\in\left[-1;1\right]\)
\(\Rightarrow min=-\dfrac{3}{2}-\dfrac{1}{2}=-2\Leftrightarrow cos\left(4x+\dfrac{2\pi}{3}\right)=1\)
\(\Rightarrow max=-\dfrac{3}{2}+\dfrac{1}{2}=-1\Leftrightarrow cos\left(4x+\dfrac{2\pi}{3}\right)=-1\)
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số :
a) \(y=3-2\left|\sin x\right|\)
b) \(y=\cos x+\cos\left(x-\dfrac{\pi}{3}\right)\)
c) \(y=\cos^2x+2\cos2x\)
d) \(y=\sqrt{5-2\cos^2x\sin^2x}\)





